PPT-Perimeter, area and volume 2

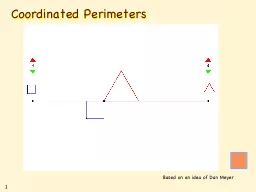
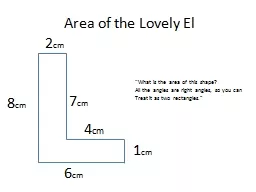
Twentyeight Checkpoint activities  Eleven additional activities Checkpoints Year 8 diagnostic mathematics activities Published in 202223 About this resource This resource is designed to be used in the classroom with Year 8 students although it may be useful for other students. Saturday 1: Geometry. Ted Coe, September 2014. cc-by-. sa. 3.0 . unported. unless otherwise noted. THE . Rules of . Engagement . Speak . meaningfully . — what you say should carry meaning; . Exhibit . Based on an idea of Dan Meyer. More or Less: Area & Perimeter. Shape Signature. The signature of a 2-D shape is the ratio of the square of the Semi-Perimeter to the Area. What is the signature of a circle? . Solve multiplicative comparison word problems by applying the area and perimeter formulas. Rename the Unit . Fluency. 7 . tens = . . . Complete . the number sentence.. 9 tens = _____. 10 tens = _____. “What is the perimeter of this shape?”. (all the angles are 90 degrees ). . Perimeter of the Lovely El. “Perimeter: the distance around an area.”. . It doesn’t have to be a “regular” shape, either. . Imagine that you and the other members of your group are a team of picnic basket ants, and you have just reached a picnic basket filled with supplies and food.. Suppose that you are small, but you walk on long, narrow feet that are the size and shape of paper clips! . This is to help you review for the . Chapter 1 Test.. Finding the Perimeter & Area. 1. Find the perimeter of the polygon below.. 2. Find the area of the polygon above.. 19 m. 10 m. 5 m. 13 m. Finding the Perimeter & Area. Formula. Perimeter. Is the distance AROUND . an object. Perimeter . If you started at one point and went all the way around. until you got to where you started, the perimeter is . the total distance you have gone.. WIDTH. WIDTH. We use the . length. and . width. measurements of a rectangle to calculate the perimeter of a rectangle.. We simply add up all the length and width measurements to find the perimeter of something.. Investigation. Take a piece of paper. Fold it in half twice. . Cut along the layers, cutting out four congruent rectangles. . 3) Find the perimeter and area of one rectangle. . 4) Place two rectangles side by side, creating a rectangle where the length was doubled. . In this lesson you will learn . that rectangles can have the same area but different perimeter . by building rectangles and organizing the information into a chart.. Perimeter tells us the distance that goes around the polygon.. Students, . Engaging . Communities. Themes . for . today: . Who,Where,. . How.. Who?. Georgia . State University . 50,000 . students, . the . largest . institution . of . higher. . education . Chemistry in a battery. More area = more power. vs.. Challenge: How can we pack a large surface area into a small space?. Length = 1. L = 1. L = 1. L = 1. Total L = 2. L = 2. L = 2. L = 2. L = 2. L = 2. What is the longest stick that fits in this cubical box?. What is the longest stick that fits in this cubical box?. Is this the only solution?. What is the longest stick that fits in this cubical box?. Java GUI. Final Code. import javax.swing.*;. import java.awt.*;. import java.awt.event.*;. import java.awt.Graphics; // program uses class Graphics. import javax.swing.JApplet; // program uses class JApplet .