PDF-On the occurrence of wave breaking Abstract Introduction Wave breaking criteria Kinematic

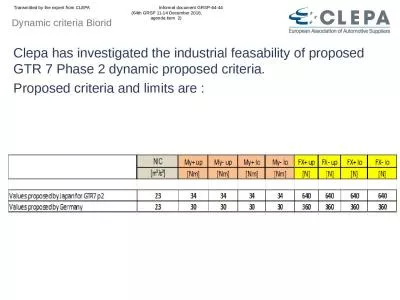
2 04 06 Nm Time UTC 123 4 m 123 4 Figure 2 Breaking scale 05 01 02 brk c 1 05 01 02 03 brk c 2 05 01 02 03 brk c 3 05 01 02 03 brk c 4 Figure 3 brPage 6br EZ EZ v 05 10 87226 10 87225 10 87224 10 87223 cc c m 87222 s Figure 4 Total breaking rate ZZ b. Thomas Herring, MIT. Room 54-820A. tah@mit.edu. . 07/11/2013. Track Kinematic. 2. Kinematic GPS. The style of GPS data collection and processing suggests that one or more GPS stations is moving (e.g., car, aircraft). Jake Blanchard. Spring 2008. Analysis of Plastic Behavior. Plastic deformation in metals is an inherently nonlinear process. Studying it in ANSYS is much like a transient problem. Instead of time steps, we have load steps. HMS. (Preliminary). March 24, 2014. Rosa Aguilar. Computational Hydraulics and Hydrology. www.mahometaquiferconsortium.org. Surface Runoff. Water flow that occurs when the soil is infiltrated to full capacity and excess water from rain, . The program-specific criteria are divided into two parts:. Curriculum. Faculty. ABET Criteria. The Context for Change. 3. Civil Engineering Body of Knowledge, Second Edition (BOK2) published by ASCE. Reading: Applied Hydrology Sections 9.3-9.7. Kinematic and Dynamic Waves. Kinematic Wave Equations. Combine (9.3.1) and (9.3.4) and after some working you get:. Analytical Solution of the Kinematic Wave. Michael . Drabkin. MD. Lauren Senior, Uma Kanth, Allison Rubin MD, Steven Lev MD. ASNR 2015 Annual . Meeting. eEdE. #: eEdE-85. Control #: 772 . Disclosures. Nothing to disclose.. Purpose. To provide the radiologist with a pattern approach to head CT interpretation based on templates of interconnected geometric shapes. The viewer is encouraged to think from general to specific and consider spatial relationships. Cases will demonstrate the utility of this framework to everyday practice.. 4. 3. 2. 1. 0. In addition to level 3.0 and above and beyond what was taught in class,  the student may:. · Make connection with other concepts in math. · Make connection with other content areas.. AP Statistics B. Overview of Chapter 17. Two new models: Geometric model, and the Binomial model. Yes, the binomial model involves Pascal’s triangles that (I hope) you learned about in Algebra 2. Use the geometric model whenever you want to find how many events you have to have before a “success”. You used proportional relationships of corresponding angle bisectors, altitudes, and medians of similar triangles. . Find the geometric mean between two numbers.. Solve problems involving relationships between parts of a right triangle and the altitude to its hypotenuse.. La gamme de thé MORPHEE vise toute générations recherchant le sommeil paisible tant désiré et non procuré par tout types de médicaments. Essentiellement composé de feuille de morphine, ce thé vous assurera d’un rétablissement digne d’un voyage sur . Delta On-Time Performance at Hartsfield-Jackson Atlanta International (June, 2003 - June, 2015). http://www.transtats.bts.gov/OT_Delay/ot_delaycause1.asp?display=data&pn=1. Data / Model. Total Operations: 2,278,897. 1. Clepa has . investigated. the . industrial. . feasability. of . proposed. GTR 7 Phase 2 . dynamic. . proposed. . criteria. .. Proposed. . criteria. and . limits. are : . Transmitted by the expert from CLEPA Informal . Thomas Lund. NorthWest. Research Associates. Boulder, CO. Boulder Fluids Seminar. 14 October, 2014. Outline. Introduction. What are gravity waves?. How are they similar/dissimilar to surface waves?. demigration. of reflections in . prestack. seismic data. Einar Iversen, NORSAR. Martin Tygel, UNICAMP. Bjørn Ursin, NTNU. Maarten V. de Hoop, Purdue University. E. Iversen et al., ROSE meeting, Trondheim, 23-24 April 2012.