PDF-Lecture notes on WavesSpectra Noise Correlations and

Author : alida-meadow | Published Date : 2014-12-11

W Gekelman Lecture 5 March 27 2004 brPage 2br The spectra can tell us if there is a signal present in the data nd what the frequencies of the waves which are in

Presentation Embed Code

Download Presentation

Download Presentation The PPT/PDF document "Lecture notes on WavesSpectra Noise Corr..." is the property of its rightful owner. Permission is granted to download and print the materials on this website for personal, non-commercial use only, and to display it on your personal computer provided you do not modify the materials and that you retain all copyright notices contained in the materials. By downloading content from our website, you accept the terms of this agreement.

Lecture notes on WavesSpectra Noise Correlations and: Transcript

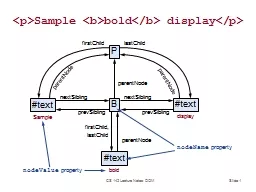
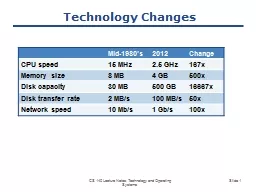
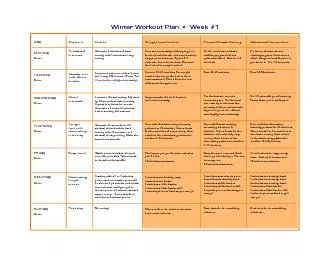
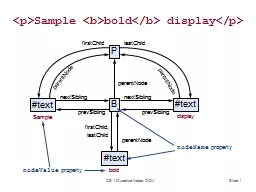
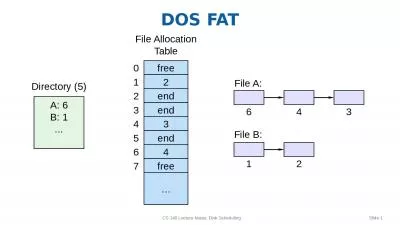
W Gekelman Lecture 5 March 27 2004 brPage 2br The spectra can tell us if there is a signal present in the data nd what the frequencies of the waves which are in the noise Are there other techniques we can use that tell us more about the waves in the. Correlation Objectives i Calculate correlations i Calculate correlations for subgroups using split file i Create scatterplots with lines of best fit for subgroups and multiple correlations Correlation The first infer Slide . 1. <. p>Sample . bold display. P. B. #text. #text. nextSibling. prevSibling. nextSibling. prevSibling. firstChild. lastChild. parentNode. parentNode. parentNode. Fernando . G.S.L. . Brand. ão. ETH Zürich. Based on joint work with . Michał. . Horodecki. . Arxiv:1206.2947. Q+ Hangout, February 2012. Condensed (matter) version of the talk. Finite correlation length implies correlations are short ranged. Pasring. Reporters: R98922004 . Yun-Nung. Chen,. R98922033 Yu-Cheng Liu. Reference. Ming Actor Correlations with Hierarchical Concurrence Parsing (ICASSP 2010). Kun Yuan, . Hongxun. Aditi. . Sen. (De). Harish-Chandra Research Institute, India. Monogamy of Quantum Correlations. Aditi. . Sen. (De). Harish-Chandra Research Institute, India. Co-workers: . Asutosh. , . Salini. , . Slide . 1. Google Datacenter. CS 142 Lecture Notes: Datacenters. Slide . 2. Datacenter Organization. Rack:. 50 machines. DRAM: 800-3200GB @ 300 . µs. Disk: 100TB @ 10ms. Single server:. 8-24 cores. DRAM: 16-64GB @ 100ns. Slide . 1. Technology Changes. Mid-1980’s. 2012. Change. CPU speed. 15 MHz. 2.5 GHz. 167x. Memory size. 8 MB. 4 GB. 500x. Disk capacity. 30 MB. 500 GB. 16667x. Disk transfer rate. 2 MB/s. 100 MB/s. Day Monday Notes: Tuesday Notes: Wednesday Notes: Thursday Notes: Friday Notes: Saturday Notes: Sunday Notes: Workout Intervals Steady row Repeat four times for one set then take a break of 3 minu Slide . 1. <. p>Sample . bold display. P. B. #text. #text. nextSibling. prevSibling. nextSibling. prevSibling. firstChild. lastChild. parentNode. parentNode. parentNode. Slide . 1. Access Matrix. File A. File B. File C. Printer 1. Alice. RW. RW. RW. OK. Bob. R. R. RW. OK. Carol. RW. David. RW. OK. Faculty. RW. RW. OK. CS 140 Lecture Notes: Protection. Slide . 2. Access Matrix. Slide . 1. CSS Rule. body {. font-family: Tahoma, Arial, sans-serif;. color: black;. background: white;. margin: 8px;. }. Selector. Declaration. Block. Attribute Name. Value. CS 142 Lecture Notes: CSS. Slide . 1. Introduction. There are several good reasons for taking . CS142: Web Applications. :. You will learn a variety of interesting concepts.. It may inspire you to change the way software is developed.. Slide . 1. free. File Allocation Table. A: 6. B: 1. .... 6. 4. 3. 0. 1. File A:. File B:. Directory (5). 2. end. 2. 3. end. 3. 4. 5. end. 4. 6. 7. free. …. 1. 2. Disk Scheduling. CS 140 Lecture Notes: Disk Scheduling. Xiaoyang. . Zhuang. Economics 201FS. Duke University. 2/23/2010. Motivation. The Problem. In a crisis, . “correlations go to 1.”. For portfolio managers, converging correlations throw off diversification and hedging strategies..

Download Document

Here is the link to download the presentation.
"Lecture notes on WavesSpectra Noise Correlations and"The content belongs to its owner. You may download and print it for personal use, without modification, and keep all copyright notices. By downloading, you agree to these terms.