PDF-DivideandConquer Matrix Factorization Lester Mackey Am

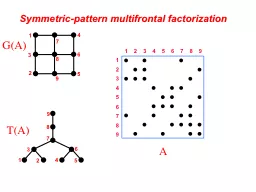
Jordan a b Department of Electrical Engineering and Computer Science UC Berkeley Department of Statistics UC Berkeley Abstract This work introduces DivideFactorCombine DFC a paral lel divideand conquer framework for noisy matrix factorization DFC d. The Cholesky factorization of allows us to e64259ciently solve the correction equations Bz This chapter explains the principles behind the factorization of sparse symmetric positive de64257nite matrices 1 The Cholesky Factorization We 64257rst show While the former has received a great deal of attention in the literature the latter is seldom analyzed and is typically borrowed without justi64257cation from the PCA context In this work we demon strate that the standard PCA de64258ation procedure Tomohiro I, . Shiho Sugimoto. , . Shunsuke. . Inenaga. , Hideo . Bannai. , Masayuki Takeda . (Kyushu University). When the union of intervals [. b. 1. ,. e. 1. ] ,…,[. b. h. ,. e. h. ] equals [1,. T(A) . 1. 2. 3. 4. 6. 7. 8. 9. 5. 5. 9. 6. 7. 8. 1. 2. 3. 4. 1. 5. 2. 3. 4. 9. 6. 7. 8. A . 9. 1. 2. 3. 4. 6. 7. 8. 5. G(A) . Symmetric-pattern multifrontal factorization. T(A) . 1. 2. 3. 4. 6. 7. 8. under Additional Constraints. Kaushik . Mitra. . University . of Maryland, College Park, MD . 20742. Sameer . Sheorey. y. Toyota Technological Institute, . Chicago. Rama . Chellappa. University of Maryland, College Park, MD 20742. by Carol Edelstein. Definition. Product. – An answer to a multiplication problem.. . 7 x 8 = 56. Product. Definition. Factor. – a number that is multiplied by another to give a product.. . 7 x 8 = 56. Barrie Lester. WHEN. 20. th. September 4pm. WHERE. The Hoppers Club. For all enquiries contact Barrie. 0421 981 511. . barrie.lester@aerobowls.com. PowerPoint by Agnes, Becky and Roanna. Key Questions. What is the character’s appearance? . She doesn’t fit in with the crowd, looks strange, different, dresses in dull clothes and seems dark at times due to her makeup.. m. movies. v11. …. …. …. vij. …. vnm. V[. i,j. ] = user i’s rating of movie j. n . users. Recovering latent factors in a matrix. m. movies. n . users. m. movies. x1. y1. x2. y2. ... ... …. Review Questions. 1. What kinds of stories did Lester tell to amuse the new employees?. The kinds of stories that Lester would tell to amuse the new employees would be the stories about the old days.. Review Questions. 1. What kinds of stories did Lester tell to amuse the new employees?. The kinds of stories that Lester would tell to amuse the new employees would be the stories about the old days.. Gemar. 11-10-12. Advisor: Dr. . Rebaza. Overview. Definitions. Theorems. Proofs. Examples. Physical Applications. Definition 1. We say that a subspace S or . R. n. is invariant under . A. nxn. , or A-invariant if:. Everyday Math Lesson 1.9. Lesson Objectives. I can tell the difference between powers of ten written as ten raised to an exponent. .. I can show powers of 10 using whole number exponents. . Mental Math. Sebastian . Schelter. , . Venu. . Satuluri. , Reza . Zadeh. Distributed Machine Learning and Matrix Computations workshop in conjunction with NIPS 2014. Latent Factor Models. Given . M. sparse. n . x .