PDF-Figure1:Examplesofsevenunboundeddependencyconstructions(a–g).Arcs

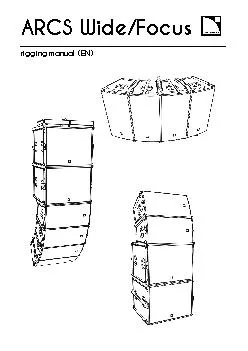
RASPparserBriscoeetal2006usingamanuallyconstructedgrammarandastatisticalparseselectioncomponentandtheDCUpostprocessorofPTBparsersCahilletal2004usingtheoutputoftheCharniakandJohnsonreranki. Pg 603. Central Angle. An angle whose vertex is the center of the circle. Arcs. Minor Arc. CB. Major Arc. BDC. Semicircle. Endpoints of the arc are a diameter. Measures of Arcs. Minor Arc. The measure of the central angle. Arc Measure. Arc Measure = the angle measure . Task 12.1. Visual Aid. http://www.mathopenref.com/arcangle.html. Central Angles & Arc Measures. Minor/Major Arcs. Minor Arcs = arcs that are less than 180°.. Auroral. Arcs. By Sarah Bender. Mentor: Kyle Murphy. 8/7/2014. Introduction. Figure . 1: . The interaction of the solar wind with the Earth’s magnetosphere.. Magnetic Reconnection. Substorms. An . subgraphs. , and feedback arc sets in . Eulerian. digraphs. Raphael Yuster. joint work with. Asaf Shapira. Eilat. . 2012. 2. Eulerian Digraph. : . A digraph in which the in-degree equals the. out-degree at each vertex.. Combiner BoxCombiner BoxInverter ––++ Combiner Box –––+++ Combiner BoxInverter ––+ 600 Vdc (Grounded System)600 and 1000 Vdc (Ungrounded System)1000 Vdc (Grounded Sy Proofs that K5 and K3,3 . are not planar. Copyright © R F Barrow 2009, all rights reserved. www.waldomaths.com. K. 5. K. 3,3. The Proofs that K. 5. and K. 3,3. are not planar. Complete graph with 5 nodes. U.S. Figure Skating Membership Members (Thousands)0301501801209060210 04–05158,000 01–02167,000 05–06 06–07185,000 99–00145,500 00–01156,000 03–04172,000 02–031 Combiner BoxCombiner BoxInverter ––++ Combiner Box –––+++ Combiner BoxInverter ––+ 600 Vdc (Grounded System)600 and 1000 Vdc (Ungrounded System)1000 Vdc (Grounded Sy OxidationstateNeutralOxidationstateElectronFormalElectronFormalCarbonyl(M–CO)Halogen(M–X)–1Phosphine(M–PRAlkyl(M–R)Amine(M–NRAryl(M–Ar)Amide(M–NR–1acyl(M&# Cotnt Area BEL AS AS ICI AD Algebra I 20–1 43–1 50–1 54–1 Biog 20–1 50–1 54–1 it 2014 44–1 50–1 58–1 SAS Standards AlignedSystem Submitted to: . Prof. Dr. Sahand Daneshvar. Presented by. : Lutfiyah Alriqeeq 16500017 . IENG516 Network Flows. Spring 2017. Definition:. An n x n assignment problem defined as:. Minimize . c. ij . rigging manual (EN) D ocument reference: ARCSWIFO_RM_EN_ 8.0 Distribution date: July 23, 2018 Get complete detail on C1000-150 exam guide to crack IBM Cloud Pak for Business Automation v21.0.3 Administration. You can collect all information on C1000-150 tutorial, practice test, books, study material, exam questions, and syllabus. Firm your knowledge on IBM Cloud Pak for Business Automation v21.0.3 Administration and get ready to crack C1000-150 certification. Explore all information on C1000-150 exam with number of questions, passing percentage and time duration to complete test. To find circumference and arc length. 7-6 Circles and Arcs . M11.C.1. Vocabulary. In a plane, a . circle. is the set of all points equidistant from a given point called the . center. . You name a circle by its center. Circle P (OP)..