PPT-Number Theory CSE 311 Autumn 2020

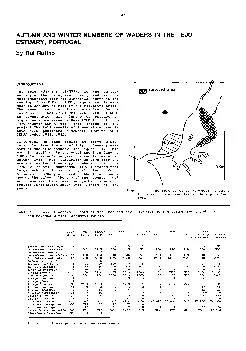
Lecture 11 httpsabstrusegoosecom353 Announcements Lots of folks sounded concerned about English proofs in sections THATS NORMAL English proofs arent easy the first few times or the next few timessometimes not even after a decade . That can lead to either increasing the clock speed or decreasing the power consumption Multiprocessing can be also used to increase speed or reduce power brPage 2br YORK UNIVERSITY CSE4210 Pipelining ab yn xn2 xn1 xn tion multiplica one and additi The autumn juvenile season can start as early as September and is busy through until the end of November However some will struggle on and the occasional one can be found from December through until April The season will vary slightly depending whet 12" 311 x 3/4" Panel with 1 lanced strips - NO Beads2% open area / Sq Ft = 2.88 Sq In. open area311-.75-0B-2L12" 311 x 3/4" Panel with 2 lanced strips - NO Beads4% open area / Sq Ft = 5. Lecture 12. Modular Arithmetic and Applications. Autumn . 2012. Autumn 2012. CSE 311. 1. Announcements. Reading assignments. Today and Friday: . 4.1-4.3 . 7. th. Edition. Howl ‘N Prowl Autumn Dog Walk. Families and their dogs come together for a few hours during the day and complete a one mile walk to honor the care giving qualities of their canine "Best Friends" and cancer survivors.. CSE 2331/5331. Topic 10:. Basic Graph Alg.. . Representations . Basic traversal algorithms. . Topological . sort. . CSE 2331/5331. What Is A Graph. Graph G = (V, E). V: set of nodes. E: set of edges. Lecture 20. Context-Free Grammars and Languages. Autumn 2012. Autumn 2012. CSE 311. 1. Announcements. Reading Assignment. 7. th. Edition, . Section 9.1 and pp. 594-601. 6. th. Edition, . Section 8.1 and pp. 541-548. Staying Overnight in Paid Accommodations. January 2015. Prepared for:. Gulf Shores and Orange Beach Tourism. by:. Table of Contents . Introduction. 3. Key Findings. 6. Detailed Findings. 10. Travel Planning. We believe that there are a number of reasons for this including late & insufficient advertising, but also that it is harder to justify a single day meeting now, when many meetings are competing for attention. CSE 490c. 10/1/2018. University of Washington, Autumn 2018. 1. Administrivia. Office Hours. Richard Anderson, Wed, 2:30-3:20, CSE 582. Samia Ibtasam, Tues, 4:00-4:50, CSE 007. Naveena Karusala, Mon, 4:00-4:50, CSE 220. Instructor:. Hal Perkins. Teaching Assistants:. Tarkan. Al-. Kazily. . Renshu. Gu Travis . McGaha. Harshita . Neti. Thai Pham Forrest . Timour. Soumya . Vasisht. Yifan Xu. Lecture Outline. Course Introduction. ESTUARY, PORTUGAL by Rui Rufino INTRODUCTION The Tejo (58ø48'N 08ø57'W) is the largest estuary on the Portuguese coast, and is the most important site for wintering waders in the country. From Part 1. 2. Review of MOSFETs and BJTs. For amplification:. MOSFET in Saturation (NMOS). BJT in Active mode (NPN). 3. Current-Voltage Characteristics. BJT in Active. MOSFET in SAT. Low-Frequency Small-Signal . Here are all the necessary details to pass the H13-311 exam on your first attempt. Get rid of all your worries now and find the details regarding the syllabus, study guide, practice tests, books, and study materials in one place. Through the H13-311 certification preparation, you can learn more on the Huawei Certified ICT Associate - AI, and getting the Huawei Certified ICT Associate - AI certification gets easy.