PPT-Newton’s Interpolation

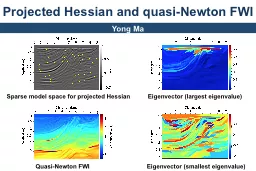
Newton Interpolation Newtons Interpolating polynomial for a set of data x 1 y 1 x 2 y 2 x 3 y 3 x m y m will turn out to be exactly the same as Lagranges Interpolating polynomial but with fewer calculations needed to construct the polynomial Newtons idea was to look for a series of constants . RENKA University of North Texas This paper presents a method of constructing a smooth function of two or more variables that interpolates data values at arbitrarily distributed points Shepards method for fitting a surface to data values at scattered To Cambridge University . sizar. in 1661 . Plague forced university to close – Newton goes home to . Woolsthorp. Annus. mirabilis of 1666. Calculus. Problem of the Moon. Dominated by Aristotle. Newton read Descartes, Galileo, . Yong Ma. Sparse model space for projected Hessian. Quasi-Newton FWI. Eigenvector (largest . eigenvalue. ). Eigenvector (smallest . eigenvalue. ). By Katherine Voorhees. Russell Sage College. April 6, 2013. A Theorem of Newton. Application and significance . A Theorem of Newton derives a relationship between the roots and the coefficients of a polynomial without regard to negative signs.. Newton’s method. Need initial guess and derivative. Quadratic convergence. Proof via . taylor’s. theorem. x_n+1 = . x_n. – f(. x_n. )/f(. x_n. ). Derivation from point-slope y = m*(x – x_0) + y_0:. Objectives. To give a definition of Interpolation as it relates to GIS and mapping/surveying. To explain How Interpolation Works. Discuss Spatial Autocorrelation, Sample Size, and Interpolation Barriers. and. Dr. Albert Einstein . 2. nd. and 8. th. period. ELAR. Books I read. I read “Isaac Newton, Organizing the Universe,”. By: William J. Boerst.. ©2004. . I also read “Albert Einstein, Giants of Science,”. Methods. (S. A. . Sahu. ). Code. : AMC 51151. Syllabus . We can divide our syllabus in following four major sections:. Method of solution of system of equations. . . . . . Solution of Non-linear Simultaneous Equations. starting . point. MATH. . 6630. By. . Morgan. . and . tajero. BACKGROUD. “Newton Method” is also called as Newton-Raphson Method, which been named by Isaac Newton and Joseph Raphson.. Newton Method was first published in 1685 . Whenever one object exerts a force on a second object, the second object exerts an equal and opposite force on the first.. “To every action there is an equal and opposite reaction”. F(AB) = - F(BA). 보간법. . (Interpolation). Page . 2. 보간법. (Interpolation). In this chapter …. 보간법이란. ?. 통계적 혹은 실험적으로 구해진 데이터들. (. x. i. ). 로부터. , . 주어진 데이터를 만족하는 근사 함수. Hui. Pan, . Yunfei. . Duan. possible problem in physical measurement . Sometimes know the value of a function f(x) at a set of points, but we don’t have an analytic expression for f(x) that lets us calculate its value at an arbitrary point. . Greg Beckham. Nawwar. . Problem Statement. Estimating function of more than one independent variable y(x. 1. , x. 2. , …, x. n. ). Complete set of values on a grid or scattered data. Outline. Grid in n-dimensions. INTerpolation. and . Abstract . interpretation. Arie. . Gurfinkel. (SEI/CMU). with . Aws. . Albarghouthi. and Marsha . Chechik. (U. of Toronto). and . Sagar. . Chaki. (SEI/CMU), and Yi Li (U. of Toronto).