PDF-Noisy Interpolation of Sparse Polynomials and Applications Shubhangi Saraf MIT shibsmit

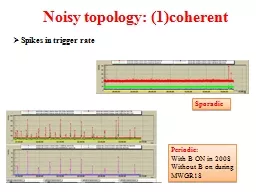
edu Sergey Yekhanin Microsoft Research yekhaninmicrosoftcom Abstract Let be a polynomial of degree q It is wellknown that can be uniquely recovered from its values at some points even after some small fraction of the values are corrupted In this pape. edu Abstract We consider the sparse Fourier transform problem given a complex vector of length and a parameter estimate the largest in magnitude coe64259cients of the Fourier transform of The problem is of key interest in several areas including s Such matrices has several attractive properties they support algorithms with low computational complexity and make it easy to perform in cremental updates to signals We discuss applications to several areas including compressive sensing data stream Chapter 15. Above: GPS time series from southern California after removing several curve fits to the data. Curve Fitting in Earth Sciences. Fitting curves to data is very common in Earth sciences. Has applications in virtually all subdiscipline. Hui. Pan, . Yunfei. . Duan. possible problem in physical measurement . Sometimes know the value of a function f(x) at a set of points, but we don’t have an analytic expression for f(x) that lets us calculate its value at an arbitrary point. . Goal: To simplify polynomial expressions by adding or subtracting. Standard: . 9.2.3.2 – Add, subtract and multiply polynomials; divide a polynomial by a polynomial of equal or lower degree.. Guiding Question: How do I simplify polynomials expressions? AND how do I add or subtract polynomials expressions?. A science story. Darin J. . Ulness. Department of Chemistry. Concordia College, Moorhead, MN. Spectroscopy. Using . light. to gain information about . matter. Spectra. Transition frequencies. Time dynamics. . Michael Elad. The Computer Science Department. The Technion – Israel Institute of technology. Haifa 32000, Israel. MS45: Recent Advances in Sparse and . Non-local Image Regularization - Part III of III. . menakjubkan. . bila. . mengingat. . bahwa. . tubuh. . memberi. . gula. & . asam. amino . kepada. . otak. , . dan. . hasilnya. . adalah. . puisi. & . tarian. ROBERT COLLINS. OTAK: SUMBER PIKIRAN & KEPRIBADIAN. Author: . Vikas. . Sindhwani. and . Amol. . Ghoting. Presenter: . Jinze. Li. Problem Introduction. we are given a collection of N data points or signals in a high-dimensional space R. D. : xi ∈ . Lesson Objective: NCSCOS 1.01 – Write the equivalent forms of algebraic expressions to solve problems. Students will know the terms for polynomials.. Students will know how to arrange polynomials in ascending and descending order.. Georgina . Hall. Princeton, . ORFE. Joint work with . Amir Ali Ahmadi. Princeton, ORFE. 1. 5/4/2016. IBM May 2016. Nonnegative and convex polynomials. A polynomial . is nonnegative if . How does . nonnegativity. Interpolating a temperature surface. 1. Problem. SOLUTION. Interpolation - applications. Interpolating a rainfall surface. SOLUTION. Problem. Interpolation - applications. Interpolating a landscape surface. Spikes in trigger rate. Periodic:. With B ON in 2008 . Without B on during MWGR18 . Sporadic . MWGR 19. Strip noise profile. 6 may . 22 April. REASON: HV problem in RB1 out sect 12. Noisy topology. Bayu . fajar PRATAMA. Bunga Amilia. Fadilayana damanik. Fanny pratiwi. Fika maulidah. Meiliza Rausan. Nelli sapitri. Rica dhamayanti. Welly natanael. Zhana daisya. Lho Kok Loyo ?. Learning Issue. Neuroanatomi.