PDF-led Cartesian tra

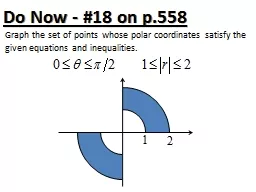
Ky Kz 3D randoml y unde r sam j ector Figure 2 Random undersampling by randomly removing p haseencodes Figure 1 Wavelet coefficients interference distribution Large scale wavelets corresponds. LED Liquidators Inc. is an industry leader in the sale of high quality LED lighting products.  We are a U.S. Veteran owned and operated company that values honor, integrity, and service. http://www.ledliquidatorsinc.com | We are large project specialists with expertise in industrial and commercial buildings and facilities, retail stores, restaurants, museums and public buildings, schools and universities, financial institutions, landscaping projects and much, much more. From custom beam angles and kelvin temperatures to expert installation advice, we are here to help you with your next project. In each ordered pair the 64257rst component is an element of and the second component is an element of Example Cartesian product If and ab cd then ab cd ab cd Determining If and are 64257nite sets then 57527 because there are choices for the Vectors in three space. Team 6:. Bhanu Kuncharam. Tony Rocha-. Valadez. Wei Lu. The position vector . R. from the origin of . Cartesian coordinate system. to the point (x(t), y(t), z(t)) is given by the expression. Presented By:. Loris D’Antoni . Joint work with:. Margus. . Veanes. Outline. Symbolic Automata and Transducers. Extended Symbolic Automata and Transducers. Some negative results. Some positive results. Week - . Miami. 4 . - 6 . MarZO . 2013 . ASPETTI FISCALI e SOCIETARI DELL’ACQUISTO DI IMMOBILI NEGLI USA . PRESENTED BY:. ESCLUSIONE RESPONSABILITA’. Diniego. di . responsabilità. : Il . materiale. Part I: Polar Coordinates. Objectives. Objectives: Know how to convert between polar and Cartesian coordinates and how to sketch functions in polar coordinates. Corresponding Sections in Simmons 16.1,16.2,16.3. Dott. Marco . Teti. Università degli Studi di Ferrara. marco.teti@unife.it. Premessa. R. ealizzando . Batman. (1989) e . Batman – Il ritorno. (. Batman . Returns. , 1992) Tim Burton esplora, seppure in maniera originale e insolita, “territori” narrativi tutt’altro che sconosciuti ai registi cinematografici, soprattutto americani. La trasposizione filmica di opere a fumetti è da oltre un secolo una pratica consueta sia negli Stati Uniti che in Europa. . Gra. ph the set of points whose polar coordinates satisfy the. g. iven equations and inequalities.. Relating Polar and Cartesian Coordinates. Section 10.5b. Relating Polar and Cartesian Coordinates. Coordinate Conversion. Definition, Discrete Forms, Examples . A.D. . . Rollett. 27-750. Texture, Microstructure & Anisotropy. Updated . 27. th. . Jan. 2016. 2. Lecture Objectives. Introduce the concept of the Orientation Distribution (. David Fleet. We need many clusters. Increasing . number of . clusters. Problem: . Search time, storage . cost . (subspace 1). (subspace 2). (subspace 1). (subspace 2). (subspace 1). (subspace 2). (subspace 1). A time for teachers to meet with needs/skill-based groups . This is especially important for students with specific skill-gaps necessary for success in your classroom. . Could be used for…. Pre-teaching or Re-teaching. Brand with . long. . tradition. – . over. 30 . years. on the market. Brand . recognized. by . customers. BASIC PORTFOLIO. Good. . value. for . money. . LED . replacement. of the most popular . Indoor LED signs are becoming increasingly popular as a form of advertising due to increased familiarity with the digital world. Call us!