PDF-Perpendiculars in a Cyclic Quadrilateral

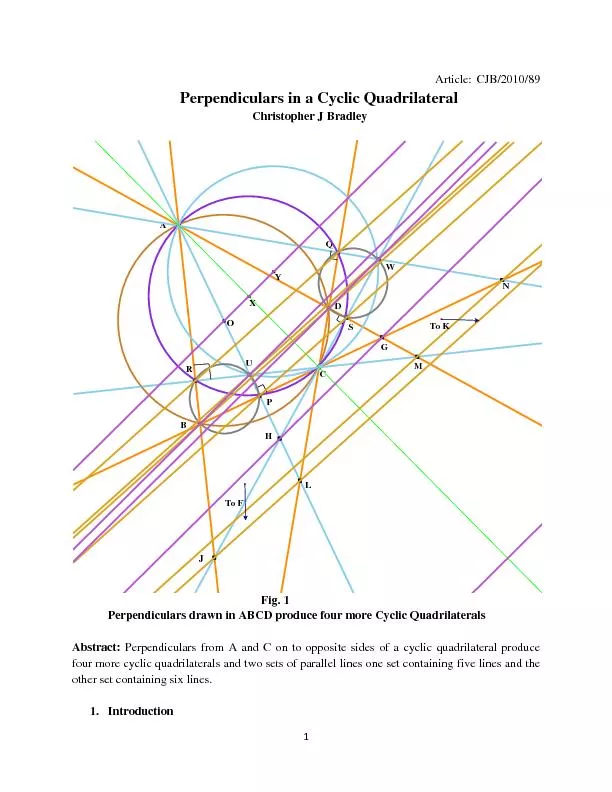
1 Article CJB201089 Christopher J Bradley Fig 1 Perpendi culars drawn in ABCD produce four more Cyclic Q uadrilaterals Abstract Perpendiculars from A and C on to opposite sides of a cyclic qua. Leftseat 57375ight controls are removable PISTOLGRIP CYCLIC Ergonomic grips incorporate two position trigger switches for intercom and transmit Pilotside grip features buttons for convenient switching of J The ROBINSON R44 RAVEN SERIES provides exc Dan Archdeacon. The University of Vermont. Common goal: . Embed a simple graph such that . every face is a triangle. Why?. Minimizes the genus of the embedding. Examples include . n = 0,3,4,7 (mod 12). 2. , 201. 2. .0. 7.02.. . – . R. z. es. zó. w. , . Poland. Gergely . Wintsche. Generalization. through. . problem. . solving. Gergely . Wintsche. Mathematics Teaching and Didactic Center. P. 546-549: 1, 2, 3-30 M3, 32, 34, 36, 39, 41, 44, 45. P.733-6: 3, 12, 13, 17, 21, 24, 26, 43. Almost a Trapezoid Worksheet. 8.5: Use Properties of Trapezoids and Kites. Objectives:. To discover and use properties of trapezoids and kites. applications. The 10th IEEE Conference on Industrial Electronics and Applications (ICIEA 2015. ), Auckland , 15-17 June 2015. Kai Ki Lee. 1. ,Ying Kin Yu. 2. and Kin Hong . Wong. 2+. 1. Dept. of Information Engineering, The Chinese University of Hong Kong (CUHK). Created By: 2BrokeTeachers. A Parade of Four-Sided Polygons. Quadrilaterals. There are many different types of quadrilaterals. We identify quadrilaterals using their sides and angles. . Side. Angle. Let’s Review…. Characteristics of a rectangle:. Both sets of opp. Sides are congruent and parallel. Both sets opp. angles are congruent. Diagonals bisect each other. Diagonals split it into 2 congruent triangles. Consecutive angles are supplementary. What makes a quadrilateral a rhombus?. Rhombuses Or Rhombi. A . rhombus. . is an equilateral parallelogram.. All sides are congruent. Rhombus Corollary. A quadrilateral is a rhombus if and only if it has four congruent sides.. both pairs of opposite sides are . both pairs of opposite . ∠. s are . diagonals bisect each other. any pair of consecutive . ∠. s is supplementary. 1.  .  . Types of Parallelograms. rectangle. Polygon Interior angle sum. The sum of the interior angle measures of an . n. -sided convex polygon is (n-2) 180. Po. lygon Exterior angle sum. The sum of the exterior angle measures of a convex polygon, one angle at each vertex is 360 degrees. Review Quiz . #10. Proving Theorems about . Parallelograms. Question 1. Determine whether these four vertices form a parallelogram: . A . (–3, 0), . B . (6, 0), . C . (1, 1), . D . (–2, –2).. No, because both pairs of opposite sides are not parallel.. A Parade of Four-Sided Polygons. Quadrilaterals. There are many different types of quadrilaterals. We identify quadrilaterals using their sides and angles. . Side. Angle. Let’s Review…. All polygons are made up of line segments and angles. The line segments that create quadrilaterals will be parallel, perpendicular, OR intersecting.. quadrilateral. trapezoid. parallelogram. rectangle. rhombus. square. What is this?. trapezoid. (and quadrilateral). What is this?. parallelogram. We shall learn how to construct a unique quadrilateral by following methods :-. When four sides and one diagonal are given.. When two diagonals and three sides are given.. When two adjacent sides and three angles are given..