PDF-JOURNAL OF FUNCTIONAL ANALYSIS 86

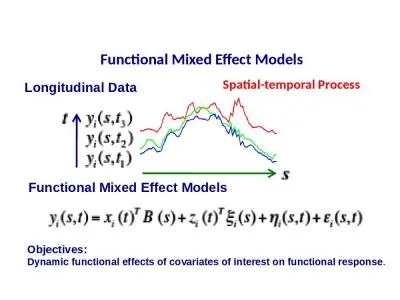
136179 1989 On Peak Sets for Lip a Classes ALAN V NOELL Department of Mathematics Oklahoma State University Stillwater Oklahoma 74078 AND THOMAS II WOLFF Department Mathematics 253. H Mason David Mouillot William G Lee and J Bastow Wilson Mason N W H Mouillot D Lee W G and Wilson J B 2005 Functional richness functional evenness and functional divergence the primary components of functional diversity Oikos 111 112 118 Functional Vs. Aesthetic. Design. Functional Design. A functional design occurs when an item is designed to fulfil a need or purpose. it is constructed so that it works for the occasion for which it was created.. Objective: . To compare and contrast between functional and dysfunctional characteristics between families and to distinguish that no one family is ideal or measurable of perfection. . Functional. Of or relating to a function or functions. Data. . S. tructures. Purely. . functional. car. . cdr. never. . modify. only. . create. new pairs. only. . DAGs. [C. . Okasaki. , . Simple and efficient purely functional queues and . deques. Vs. Aesthetic. Design. Functional Design. A functional design occurs when an item is designed to fulfil a need or purpose. it is constructed so that it works for the occasion for which it was created.. DISCOVERING similar functional abilities in Nature. ABSTRACTING natural design principles. APPLYING design principles to generate innovation. EVALUATING design concepts according to sustainability and other criteria. C. urrencies. Coen Decnop, Business Analyst, . Infor. Dan Aldridge, Senior LN Finance Consultant. , . www.PerformaApps.com. . 2. Currency . Systems. CAD. Reference. EUR. EUR. USD. Dependent. BRL. USD. Data. . S. tructures. Purely. . functional. car. . cdr. never. . modify. only. . create. new pairs. only. . DAGs. [C. . Okasaki. , . Simple and efficient purely functional queues and . deques. Functional Subsystems. A GIS has four main functional subsystems. These are:. Data Input Subsystem. Data Storage and Retrieval Subsystem. Data Manipulation and Analysis Subsystem. Output/ Display Subsystem. IN THE ABSENCE OF DISABILITY:. THE LYMPHEDEMA EXAMPLE. Robert Weiss, M.S.. Porter Ranch, CA. LymphActivist@aol.com. OMICS 3. rd. International Conference and Exhibition on. Physical Medicine & Rehabilitation . Functional: Of or having a special activity, purpose, or task: relating to the way in which something works or operates.. Design a functional ceramic product for a . public. . figure. .. Goals:. Concept makes sense with public figure chosen. Volume 2(1): 1-3 AbstractfMRI, which captures images reected the hemodynamic changes during the neural activity, shows great potential to uncover the with the brain function and the neuropatholog Steven L. Bressler. Cognitive Neurodynamics Laboratory. Center for Complex Systems & Brain Sciences. Florida Atlantic University. Overview. EEG Source Imaging IOP 2016. 1. Functional Connectivity of macaque cortical LFPs. Functional Mixed Effect Models. Spatial-temporal Process. Longitudinal Data. Objectives:. Dynamic functional effects of covariates of interest . on functional . response. .. FMEM. Global Noise Components.