PDF-Proceedings of the Stockholm Music Acoustics Conference, August 6-9, 2

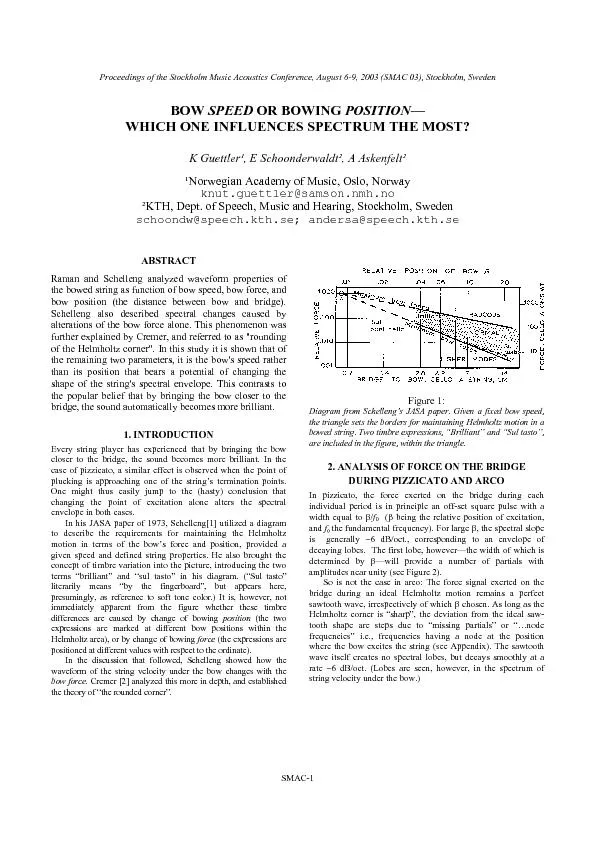
BOW SPEED OR BOWING POSITION151 WHICH ONE INFLUENCES SPECTRUM THE MOST K Guettler. Proceedings of the Music and Music Science Conference (2005)special sort of brain-state.Over the past twve begun to takscience. Somehave begun to apply the lessons of cognitive science to traditional Time-Reversed Acoustics November 1999 91 ACOUSTICSArrays of transducers can re-create a sound and send it back to its sourcestones, detect defects in materials and communicate with submarinesby M David Canning. Hear2Learn. http://tinyurl.com/UCLAPDCA. Management of APD. Educational Video 1953. Learning points:. Noise in classrooms is usually generated within the classroom by the children and adults present.. Jansson: Acoustics for violin and guitar makers page 8.3 In this part fundamentals of the tone production of the violin will be presented, i.e. the road from bow via the violin to the tone radiated i . FEATS 2008 - Stockholm. *. supporting seagulls played by ABBA and vicarious Vikings. Stage. Top of Stage. 0.6m. 1.4m. 2m. 4.5m. 6.5m. Therefore. Length of wire = (4.5 x 2) + 0.6. = 9.6 ~ 10m. x 3 = 30m. Cosmic parallax. Syksy Räsänen. University of Helsinki. Department of Physics. . and. The Helsinki Institute of Physics. 1. arXiv:1312.5738. AlbaNova, University of Stockholm, May 13, 2014. Change of viewpoint. Kovalevskaya. 1850-1891. A 19. th. century pioneer for women in mathematics. June Barrow-Green. The Open University. Florence Nightingale Day. Lancaster University. 17 December 2015. Hypatia. of Alexandria. Presentation at Competition Day, Bratislava. Benoît Durand. benoit.durand@rbbecon.com. 23 November . 2016. Total damage for direct purchasers. A. €. Quantity. B. Demand. p. 1. c. 1. c. 0. q. 1. p. Molly Wood, P.E.. USGS Idaho Water Science Center. Snake River nr . Anatone. , WA. Clearwater River at Spalding, ID. Kootenai River, ID – multiple locations. Boise River near Parma, ID. 6 surrogate gages w/acoustics. acoustic. ”. The word "acoustic" is derived from the . Greek. word ἀκουστικός (. akoustikos. ), meaning "of or for hearing, ready to hear“. .. The Latin synonym is "sonic", after which the term . SOME BASICS OF. ARCHITECTURAL ACOUSTICS. Auditorium Acoustics. Science of Sound. , Chapter 23. Principles of Vibration and Sound. , Chapter 11. Kimmel Center. Free field. Reflections. p . vs. r. log . acoustic products’ design, launch and technical support. Our company has over 20 years of experience. We creatively combine modern acoustics techniques and marketing ideas. Going beyond single pr SB15m SB15 m SUBWOOFER rigging manual VERSION 1.0 www.l - acoustics.com 2 Document reference: SB15m _RM_EN_1.0 Distribution date: March 21, 2017 May 8, 2018. Chair: Frederick J. . Gallun. VA RR&D NCRAR. 175. th. ASA Meeting, Minneapolis, MN Spring 2018. Agenda. Introduction . of Current PPTC Members. Election of New TC Members. Acknowledgment of PPTC .