PDF-An analytical approach to optimize AC biasing of bolometers Andrea Catalano Alain Coulais

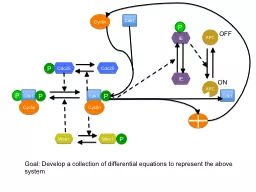
univparis7fr Bolometers are most often biased by Alternative Current AC in or der to get rid of low frequency noises that plague Direct Current DC amp li64257cation systems When stray capacitance is present the responsivity of the bolometer di64256er. acat Univ Paris Diderot Sorbonne Paris Cite LIAFA CNRS UMR 7089 Paris ceneasighirea liafaunivparisdiderotfr Abstract We present a shape analysis for programs that manipulate overlaid data structures which share sets of objects The abstract domain con 1.The unmodi Academic Programs Committee Philosophy. The Academic . Programs . Committee (APC) will carry out its responsibility consistent with the University of South Florida Sarasota-Manatee (USFSM) and its functions. . Academic Programs Committee Philosophy. The Academic . Programs . Committee (APC) will carry out its responsibility consistent with the University of South Florida Sarasota-Manatee (USFSM) and its functions. . p. ar . Thierry Leclerc. thierryleclerc@hotmail.com. 06 23 57 15 39. . . «.  Paris est de toutes les villes la moins modeste… Impossible d’ouvrir le poste de radio sans entendre Paris se louer par l’entremise d’une chanson… », écrivait Jean Cocteau. . Basis of amplifiers. Obtaining linear amplification. Small-signal voltage Gain. Equivalent-circuit models: . π. model and T model. Basic configurations and Biasing. Analyze discrete-circuit amplifiers. Simon Dicker. MUSTANG . MUSTANG. 64 absorber coupled TES bolometers . 45” field of view . Cold reimaging optics. Bare pixels (0.7 f*lambda). Time Domain multiplexed readout. 300mK cryogenics running off a PT405. Basis of amplifiers. Obtaining linear amplification. Small-signal voltage Gain. Equivalent-circuit models: . π. model and T model. Basic configurations and Biasing. Analyze discrete-circuit amplifiers. travel industry . as Director, . Market Research . at the . U.S. . Travel Association in Washington DC. She . originally . hails from Minneapolis, . Minnesota and currently . resides in Maryland with her husband, son, and daughter. Mathew Willmott. California Digital Library. 3. rd. ESAC Workshop:. On the Effectiveness of APCs. June 29, 2018. About CDL/UC. About CDL/UC: Background. Serves 190,000 faculty and staff and 239,000 students across the 10 campuses of the University of California system. Sapunenko. On behalf of INFN-T1 staff. HEPiX spring 2012. Outline. Facilities. Network. Farming. Grid and Middleware. Storage. User experience. 2. 24-apr-2012. Andrea Chierici. INFN-Tier1: numbers . 1000 m. HER BACKGROUND. Graduated from high school as valedictorian. Captain of the swim team. Officer in the National Honor Society. Worked as a registered nurse at the University of Texas M.D. Cancer Center from 1986 – 1994. 1. ND 280 upgrades . with. help by Etam Noah, Jeanne Wilson, Mark . Hartz. , Leila . Haegel. , Mark . Rayner. , . Minamino. , Ichikawa, and . many. . others. . 6 August 2015. ND280 upgrades Alain Blondel T2K meeting 3June15 . APC. P. Cdk1. Cyclin. P. P. Cdk1. Cyclin. P. P. Cdc25. Wee1. Wee1. P. IE. Cdk1. OFF. ON. Goal: Develop a collection of differential equations to represent the above. system. Cyclin. Cdk1. Cdc25. IE. APC.