PDF-8.2Non-LinearCurve(e.g.,Parabola)Firstly,letustabulatesomepairsofvalue

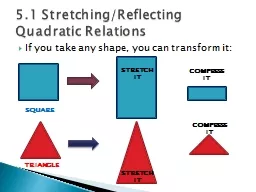
x 4 3 2 1 0 1 2 3 4 y 16 9 4 1 0 1 4 9 16 yx2Nowplotthepointsrepresentingthesenumberpairs Observethatinthequadraticfunctionfxx2fortheparabolawehavewrittenyinsteadoffxieyfxSome. 2Non-ionisingradiationIncontrasttoourknowledgeontheunderlyingmecha-nismsofIR-inducedbiologicaleffects,theexperimentaldataregardingbiologicaleffectsofchronicexposuretonon-ionisingradiation(NIR)attypica Warm Up. 13. 2. . from (0, 2) to (12, 7). Find each distance.. 3. . from the line . y. = –6 to (12, 7). 13. 1. . Given . , . solve for . p. when . c. =. Write the standard equation of a parabola and its axis of symmetry.. We already know A LOT about parabolas. 2 forms (standard and vertex). How to find Vertex (. h,k. ) or (-b/2a). Axis of Symmetry. Characteristics. Many ways to solve their equations. Solutions are x intercepts. Section 2.3 beginning on page 68. The Big Ideas. In this section we will learn about…. T. he focus and the . directrix. of a parabola. Writing equations for parabolas using the focus, the . directrix. Factor: 3x. 2. + 10x + 8. Factor and Solve: 2x. 2. - 7x + 3 = 0. Math I. UNIT QUESTION: What is a quadratic function?. Standard: . MM2A3, MM2A4. Today’s Question:. How do you graph quadratic functions in vertex form?. We have done/worked with many variations of a parabola. The . standard form. of a parabola centered the center (h, k) is given by;. . On a parabola, every point is a . fixed . distance from a point known as the . 5.1 Stretching/Reflecting Quadratic Relations. SQUARE. STRETCH IT. COMPRESS IT. TRIANGLE. STRETCH IT. COMPRESS IT. We can transform the shape of a parabola too:. Transforming Parabolas. y = x. 2. y = 9x. Garrett . Delk. gdelk71687@csu.fullerton.edu. Department of Mathematics. CSU Fullerton. Presented at . 2013 CMC Conference. Palm Springs, CA. Parabolas and Quadratic Equations. Agenda. Welcome. CCSS. Parabolas are shaped like a U or C. Parabolas. Equations -. y-k . = a(x - h). 2. . opens up if a > 0, opens down if a < 0.. x-h. . = a(y - k). 2. . opens right if a > 0, opens left if a < 0.. Valerie Belew . History of Parabolas . Menaechmus. (380 BC - 320 BC) found the parabola. Apollonius (262 BC - 190 BC) named the parabola. Pappus. (290 - 350) found the focus and . directrix. of the parabola. Slide 1 2-5 GRAPHS OF EXPENSE AND REVENUE FUNCTIONS Find the vertex of the parabola with equation  y  = x 2  + 8 x  + 15 . Vertex formula: (-b/2a, y) Warm Ups: Slide 2 2-5 GRAPHS OF EXPENSE AND REVENUE FUNCTIONS Pencil, 60/30°, Compass Set-Square & Masking tape. Step 1: Set up and line out page as per specification. Step 2: Locate start point of parabola on the page. Step 3: Using the rectangle method, draw a rectangle using desired measurements. Note that measurements divisible by 5 are easy to work with.. ISBN 978-0-88385-767-0. Behavior of Polynomial Functions. Behavior of Polynomial Functions depend on:. Degree of the polynomial (most important). Value of the zeros. Sign of the leading coefficient. Quadratic Polynomials. Parametric Equations. 6. .1 . Introduction. The General Quadratic Equation in x and y has the form:. Where A, B, C, D, E, F are . constants.. The graphs of these equations are called . Conic Sections.