PDF-Gear Catalog ENGINEERING INFORMA TION SPUR GEARS GEAR NOMENCLA TURE ADDENDUM a is the

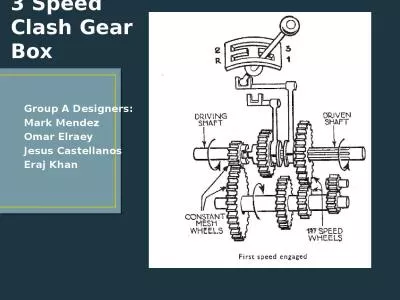
BASE DIAMETER D is the diameter of the base cylinder from which the involute portion of a tooth profile is generated BACKLASH B is the amount by which the width of a tooth space exceeds the thickness of the engaging tooth on the pitch circles As ac. 1 INTRODUCTION Gear is one of the important machine tool elements which is an integral and inevitable part of power transmission system A gear is a round blank having teeth along its periphery Gears are used to transfer powe r or torque from prime mo Spur Gear This is a cylindrical shaped gear in which the teeth are parallel to the axis It has the largest applications and also it is the easiest to manufacture 6 Spur Rack This is a linear shaped gear which ca A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 57513 2003 HighScope Educational Research Foundation 21 Language and Literacy Language and Literacy Language and Literacy Circle one Item Q R S T U V W X Circle one Level 12345 Date Observer Circ Technology. MECH: F-1. . SUBJECT. : KINEMATICS OF MECHANICS. RESPECTED FACULTY. - VATSAL SHAH . GEARS-. CONTENT. Introduction. Gears are used to transmit motion from one shaft to another or between shaft and a slide. This is achieved by successfully engaging teeth. . Introduction & History. Classifications. Nomenclature. Types of gears. Objectives & applications. Numerical Analysis. G. EARS . I. ntroduction. A . G. ear. is a . rotating. . machine. part having cut . GEAR. CONTENTS. POWER TRANSMISSION. GEAR. TYPES OF GEARS. NOMENCLATURE. APPLICATIONS OF GEARS. VELOCITY RATIO. GEAR TRAINS. EXAMPLE PROBLEMS AND QUESTIONS. GEAR. Power transmission is the movement of energy from its place of generation to a location where it is applied to performing useful work. Gears, Pulleys, & Sprockets. These three power train elements transfer energy through rotary motion. . Change the speed of rotation. Change the direction of rotation. Change the amount of torque available to do work . Information about power transmission and uses . for each type.. Robotics 101. Why do we need Gears and Pulleys?. Why do we have gears?. Why do we have pulleys?. Geek. Easy Work Can . Tow or Push. Heavy Objects!. Workshop Technology. Mansoor Ghazi, Department of Mechanical Engineering. College of E&ME, NUST Pakistan. Contents. Functions of Gears. Gear Types. Gear Nomenclature. Conventional Manufacturing Processes. Seshan brothers. Objectives. Learn about the different types of LEGO gears and what you use them for. Learn how to calculate gear ratios. Learn some useful gearing techniques. 2. What Is a Gear?. A gear is a wheel with teeth that meshes with another gear. Gears are toothed wheels. Gears are used to transmit motion. Gears are also used to convert . rotary. motion. . to linear motion or visa versa. Gears can be used to reduce or increase the . torque. GEAR. TYPES OF GEARS. NOMENCLATURE. APPLICATIONS OF GEARS. VELOCITY RATIO. GEAR TRAINS. EXAMPLE PROBLEMS AND QUESTIONS. GEAR…... Power transmission is the movement of energy from its place of generation to a location where it is applied to performing useful work. Mark Mendez. Omar . Elraey. Jesus Castellanos. Eraj. Khan. Parts: . 13. Movement: Rotation and Transfer . Spur Gears . Catalog. #. Teeth #. Pressure. Angle. Diametrical. Pitch (in). Face. (in). S412. Gears. A gear is a simple machine like a lever. The larger the diameter of the gear the longer the lever. What are Gears used for?. Ensure positive motion. Reverse the direction of rotation. Increase or decrease the speed of rotation.