PDF-IEEE TRANSA CTIONS ON MEDICAL IMA GING Primal Sk etch of the Corte Mean Curv ature Morphogenesis

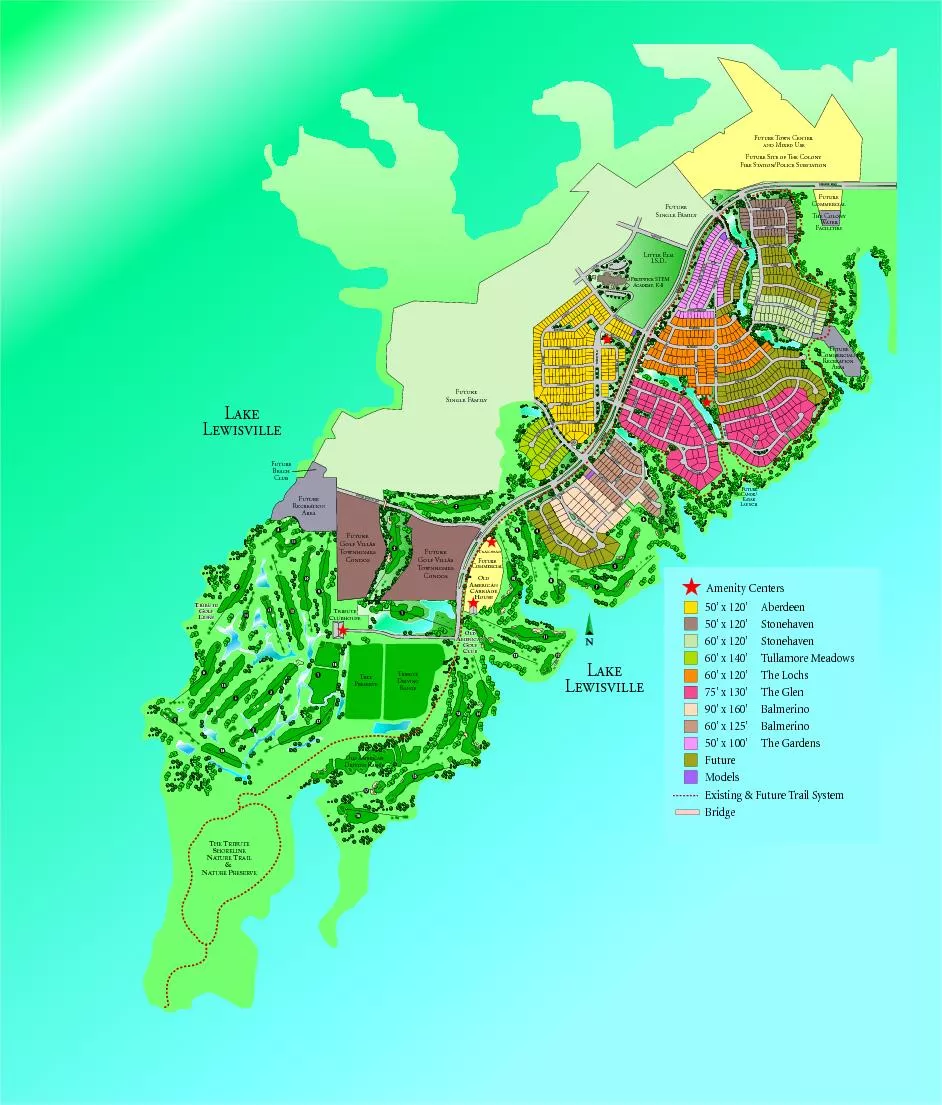
Cachia JF Mangin D Ri vi ere Kherif N Boddaert A Andrade D apadopoulosOrf anos JB Poline I Bloch M Zilbo vicius Sonigo Brunelle and J egis Abstr act In this paper we pr opose new epr esentation of the cortical surface that may be used to study the c. 00 2009 IEEE optimization effort Multicore processors based on coher ent hardwaremanaged caches provide the abstraction of a single shared address space This abstraction frees programmers from having to explicitly manage data as it moves through the . – . Integrated Development Plan Management Application. Purpose. Reports of IMA. Overview of IMA system. 2. Reports of IMA. Objective Based . Project Progress. . IMA . – Central Theme. 6. Capturing LIVE information using . Università degli Studi di Roma “La Sapienza”. C.D.L.. Ingegneria delle Nanotecnologie industriali. Corso di MEMS. A.A. 2008-2009. Professore Marco . Balucani. Ingegnere Rocco . Crescenzi. Studente:. TRAILHEADOLDAMERICANCARRIAGEHOUSE D ERICAN LF UB LDAMERICANGOLFCLUB IBUTE LF NKS RIBUTEGOLFLINKSTRIBUTECLUBHOUSE ATURE ATURE RESERVE FutureSingle FamilyFutureSingle FamilyTributeTreePreserveFutureComm Semidefinite. Programming. Satyen. Kale . (Yahoo! Research). Joint work with. Sanjeev. . Arora. . (Princeton). Semidefinite. Programming. Semidefinite. Program (SDP):. find . X. . s.t.. . Corte . Giacobbe. The Winery. Key Facts. Vineyard surface: 37 acres (15 hectares). Owner: The Dal Cero Family. Winemaker: Davide Dal Cero. Established: 1934. Location: . Roncà. Province: Verona. 9.3 Miles. Nick Reeder, May 31, 2012. Update to Scales. Changed vertical and horizontal scales on display, and added menu option to make scales equal or not.. Question: Vertical scale’s max value is 2 . m, but most of our . Most trends are not consistent. They depend on the specific values of input parameters.. At point A, pressure increases causes etch rate increase but at pint B, the trend is the inverse. Etch rate. Pressure. Cortes de poda Esquema: Di The 2019IMA Student Leadership Conference SLCwas held inCharlotte North CarolinaAccounting and Finance students from acrossthe worldmet from November 14th16thto learn more about a unique variety of to EDUCATION HISTORYName of InstitutionDegreeMajorDate Received/ExpectedUndergraduateGraduateProfessional Designations EarnedUSCPA CFA OtherCHAPTER AFFILIATIONSee a list of Regular/Student Chapte N Kumar. National co-ordinator. President, IMA Kerala. Aims and objectives. To introduce IMA to medical students and to create a professional, scientific and social outlook in them.. To facilitate academic, extra . New ways to treat or prevent lung cancer. are therefore needed.. This study explored the hypothesis that inhibition of TNKS…would inhibit lung cancer growth…. Pharmacological or genetic inhibition of TNKS1 and . For . every Medical men it becomes imperative to keep abreast of these current developments in the Medicine Arena. . In todays society with high expectations and Medical Literacy updating becomes essential ..