PPT-Laser Beams, Diffraction Gratings and Lenses

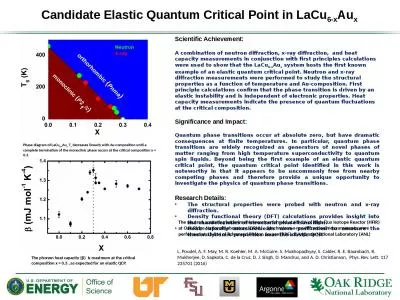
Zone plate Laserbeam diffraction A lens transforms a Fresnel diffraction problem to a Fraunhofer diffraction problem The lens as a Fourier transformer Diffraction gratings amp spectrometers. One of the big advantages to Laser Recon is that our flexible system lets us play just about anywhere…including your backyard! Now you can have the convenience of a home birthday party with an activity that will keep everyone entertained! In early 1990, Rache Corporation began developing laser technology to accurately cut thin metal shapes. Rache Corporation provides laser cutting, laser welding and Laser Marking services to a wide range of industries including medical devices, microwave components, aerospace, automotive and more. We are organized to provide cost effective laser solutions to industrial challenges in a customer-comes-first environment. Laser Recon is our form of laser skirmish, a unique sport that blends the best qualities of traditional laser tag, paintball, airsoft and video games. Guanghui Zhu. Instrument Report:. Contents. Diffraction Mechanism. C. onstruction . of . the . Diffractometer. Applications . of . XRD. Data . A. nalysis . and . Explanation. 2D XRD. XRD Simulation. Diffraction . LIGHT AMPLIFICATION by STIMULATED ELECTRON RADIATION. Question:. In movies, laser beams are always shown as bright pencils of light streaking through the air or space. If you were to look from the side at a beam from a powerful laser, would you be able to see that laser beam as it travels past you?. Diffraction of light when two fingers brought close together . infront of a light source . Diffraction by razor blade when illuminated by intense blue light . “light is never known to follow . crooked passages nor to . Chapter. 36. Copyright © 2014 John Wiley & Sons, Inc. All rights reserved.. 36-1. Single-Slit Diffraction. 36.01 . Describe the diffraction of light waves by a narrow opening and an edge, and also describe the resulting interference pattern.. Using Diffraction Gratings. Forrest . Smith. 1. , . Weliton . Soares. 2. , . Samuel . Alves. 2. , . Itamar Vidal. 2. , . Marcos . Oria. 2. . 1. State University of New York at Geneseo, . 2. Federal University of Paraiba. Marlowe,. 1. . In collaboration with: . Randall McEntaffer,. 1. . Casey . DeRoo,. 1. . Drew M. . Miles,. 1. . J. ames H. . Tutt,. 1. . Christian . Laubis,. 2. Victor Soltwisch,. 2. . Leonid . Goray. Jonathan Cowen. Swagelok . Center for the Surface Analysis of Materials. Case School of Engineering. Case Western Reserve University. . October 27, 2014. . . Outline. X-ray Diffraction (XRD). History and background. Kirigami. Nanocomposite. L. . Xu. , X. Wang. , Y. . Kim, T. C. Shyu, J. . Lyu. , N.A. . Kotov, . Kirigami. . Nanocomposites as Wide-Angle Diffraction Gratings, . ACS Nano, . 2016. 10 (6), 6156–6162.. Capella. Grating Data and the Emission Line Project - An Update. Priya Desai (CfA). Nancy Brickhouse. Jeremy Drake. Dave Huenenmoerder. Randall Smith. Andrea Dupree. Vinay Kashyap. . July 11. 6-x. Au. x. system hosts the first known example of an elastic quantum critical point. Neutron and x-ray diffraction measurements were performed to study the structural properties as a function of temperature and Au-composition. First principle calculations confirm that the phase transition is driven by an elastic instability and is independent of electronic properties. Heat capacity measurements indicate the presence of quantum fluctuations at the critical composition.