PDF-Notes on ScatteredData RadialFunction Interpolation Francis J

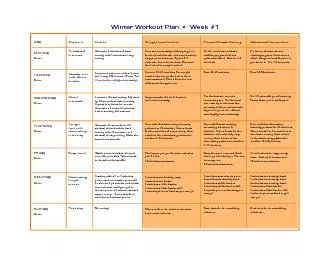
Narcowich Department of Mathematics Texas AM University College Station TX 778433368 I Interpolation We will be considering two types of interpolation problems Given a continuous function a set of vectors 1 in and scalars 1 one version of the scat. Backslash interpolation aka character interpolation character escapes escape sequences When any of these sequences are found inside a double quoted string theyre interpolated Listed on page 61 of Prog Perl Most common n t brPage 2br Translation Who is he? . What are some of the things Pope Francis has done since he has been pope?. On the next slide, enjoy some fun and interesting images of Pope Francis. . Here is Jorge . Bergoglio. riding the subway in Buenos Aires before he became pope.. Chapter 15. Above: GPS time series from southern California after removing several curve fits to the data. Curve Fitting in Earth Sciences. Fitting curves to data is very common in Earth sciences. Has applications in virtually all subdiscipline. Hui. Pan, . Yunfei. . Duan. possible problem in physical measurement . Sometimes know the value of a function f(x) at a set of points, but we don’t have an analytic expression for f(x) that lets us calculate its value at an arbitrary point. . Ji. ří. . Kadlec. . – Aalto University, Finland. . Pavel. . Treml. – Masaryk Water Research Institute and Charles University, Czech Republic. 20. .9.2013 FOSS4G. Conference. . - Nottingham. Why it’s called “regression.”. Sir Francis Galton (1822-1911). IQ testers in the early 20. th. century argued over whether Galton was . the smartest person of his day or . the smartest person who ever lived.. Day Monday Notes: Tuesday Notes: Wednesday Notes: Thursday Notes: Friday Notes: Saturday Notes: Sunday Notes: Workout Intervals Steady row Repeat four times for one set then take a break of 3 minu Objectives. To give a definition of Interpolation as it relates to GIS and mapping/surveying. To explain How Interpolation Works. Discuss Spatial Autocorrelation, Sample Size, and Interpolation Barriers. The Swamp Fox. By: José Martin Gonzales. Ju. . Hwan. . Shin. . María José Amenábar. 10-2 . An American . hero:. Who is Francis Marion?. Born in 1732 in Berkeley County, South Carolina.. Focus of Mercy. Mercy. . at. the . Heart. . of Francis’ Conversion. . PRAYER OF HIS HOLINESS POPE FRANCIS. FOR THE EXTRAORDINARY JUBILEE OF MERCY* . Misericordes. . sicut. Pater!. (Paul . Inwood. Having several close run-ins with Catholic Spanish forces when he was young caused Drake to dislike and distrust the Spanish immensely.. In his early years off the American coast Drake sailed as a slave trader and . “Heroes” by Robert Cormier Interactive Mindmaps Notes Revision Tests Sample Exam Questions How to use this presentation The next slide is you master mind map. Click on any of the coloured boxes that radiate out from the Heroes box. Dec. 23, 1869. following the publication of Galton’s . Hereditary Genius. (1869). Dec. 23. Down. Beckenham. Kent, S.E.. My dear Galton,. I . have only read about 50 pages of your book (to the Judges), but I must exhale myself, else something will go wrong in my inside. I do not think I ever in all my life read anything more interesting and . Okolie. , Prof. . Yinka. . Adekunle. & Dr. . Seun. . Ebiesuwa. . In many areas of science, we are often given a set of discrete values of a function either in the form of a table of values or a set of experimental measurements which actually represent a set of points along a .