PPT-8.4 Closures of Relations

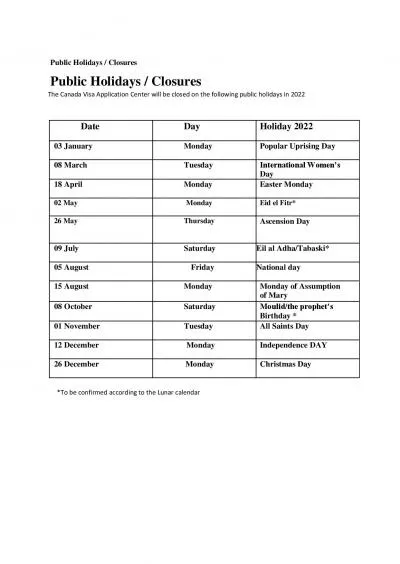
Intro Consider the following example telephone line bus route a b c d Is R defined above on the set Aa b c d transitive If not is there a possibly indirect link between each of the cities. These relations date back to ancient times There are important Indian investments in countries stretching from Oman to Egypt Sudan and beyond There have been cultural ties with the region throughout history Much of our external trade passes along th Algebraic closures We begin with one more result on algebraic extensions Lemma 151 Suppose that KF and LK are algebraic extensions Then the extension LF is also algebraic Proof In the case of 64257nitely g Things start to get serious. Telerik Software Academy. http://academy.telerik.com. . JavaScript OOP. Table of Contents. Scopes. Block and function scope. References availability. Resolving references through the scope chain. A Resource Guide for Rotary Clubs. Public Relations at its root level is all interactions that a Rotary Club has with both its members and the general public. There are four primary forms of PR communications.. INTRODUCTION TO . PUBLIC RELATIONS. Definitions of Public Relations. Public = (all) society ?. What is Public Relations?. Rex Harlow (PR educator) collected some definitions:. PR = good performance, respected by public. Paige, Taryn, Sydney, Patrick. Gator Jack’s. Public . Relations: . the influence of public opinion through proper two way communication . How does it apply to Gator Jack’s. Community participation. Heterocyclic Rings 1. (Introduction & Substitution). Ring Synthesis. Cyclization. Reactions . Cycloaddition. Reactions Ring transformation. . Baldwin's rules for ring closures . Baldwin's rules. © 2012 Cengage Learning. All rights reserved.. 1–. 2. Explain the nature, purpose, and importance of human relations.. Identify major developments in the workplace that have given new importance to human relations.. Manchester Industrial Relations Society. 19/03/15. Tim Pringle . SOAS, University of London. tp21@soas.ac.uk. MAIN . ARGUMENTS. Class struggle is driving changes to labour relations especially Guangdong . Closures. Closures. 2. Seasons. Can fish only at certain times.. Areas. Fishing restricted in specific locations. .. Fisheries. Fishing is completely . prohibited.. Marine Protected Areas (MPAs). “. Applied Discrete Mathematics Week 12: Equivalence Relations. 1. Representing Relations Using Digraphs. Definition:. A . directed graph. , or . digraph. , consists of a set V of . Quality Health Safety and Environmental Policy Silgan Closures member of Silgan Holdings Inc is a global leading supplier of metal plastic and composite closures for the food and beverages industry W Public Holidays / Closures The Canada Visa Application Center will be closed on the following public holidays in 2022 Date Day Holiday 2022 03 January Monday Popular Uprising Day 08 March T The objects of mathematics may be . related. in various ways. . A set . A. may be said to be “related to” a set . B. if . A. is a subset of . B. , or if . A. is not a subset of . B. , or if .