PDF-Signals and Systems Part In this lecture we consider a number of basic signals that will

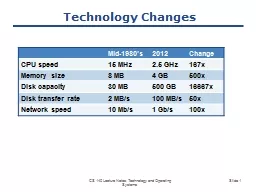
Specifically we discuss both continuous time and discretetime sinusoidal signals as well as real and complex expo nentials Sinusoidal signals for both continuous time and discrete time will be come important building blocks for more general signals. brPage 1br EEE3086F Signals and Systems II 212 Page April 14 2014 EEE3086F Signals and Systems II 212 Page April 14 2014 brPage 2br EEE3086F Signals and Systems II 212 Page April 14 201 JAMESTOWN Thur 9 th October MINLATON Thur 30 th Oct KADINA Friday 14 th November Learn Safe Drive Safe 1 Day Course Full day course to learn and complete testing to obtain a Learners Permit Fee includes a GULYHU575265734757347KDQGERRN5735957347WUDLQ -based management:. Search for . the best available . scientific evidence. The 5 steps of EBP. Formulate a focused question (. Ask. ). Search for the best available evidence (. Acquire. ). Critically appraise the evidence (. James 5:7-11. 250,000 times more likely. 25,000 times more likely. 1,300 times more likely. 18 times more likely. 3. times more likely. Life is Hard. because we live in a . fallen. world full of . sin. Minecraft. Minecraft pocket edition. Versions of Minecraft. C. rafting. Creative . mode. Minecraft Xbox edition’s. Name the block quiz. The memory quiz. Name the mobs and animals. mobs. animals. ores. Slide . 1. Technology Changes. Mid-1980’s. 2012. Change. CPU speed. 15 MHz. 2.5 GHz. 167x. Memory size. 8 MB. 4 GB. 500x. Disk capacity. 30 MB. 500 GB. 16667x. Disk transfer rate. 2 MB/s. 100 MB/s. Examples of signals:. Voltage output of a RLC circuit, stock market, ECG, speech, sequences of bases in a gene, MRI or CT scan. Examples of systems:. RLC circuit, an algorithm for predicting future of stock market, an algorithm for detecting abnormal heart rhythms, speech understanding systems, edge detection algorithm for medical images.. Trig Ghosh, PMP. Functional Manager. CGI Federal. March 13, 2012. Background. Mental Blocks. Symptoms:. State of mental impasse. Unable to respond to a situation or need. Unable to find the drive to complete a task. Georgia FIRST Tech Challenge Kickoff . 9 September 2017. FTC 7673. Dragons and Tiaras. FTC 12774 . Organized. Chaos. Towns County Schools, Hiawassee, GA. Breaking News! . . FIRST releases OnBotJava programming . Despite the extremely varied characteristics . of living organisms. , the pathways for generally . modifying and . synthesizing . carbohydrates. , . proteins. , . fats. , and . nucleic acids. are . essentially the . Instructor: . Dr. Ghazi Al Sukkar. Dept. of Electrical Engineering. The . University of Jordan. Email: . ghazi.alsukkar@ju.edu.jo. 1. Fall 2014. 2. Course Details. Objective. Establish a background in Signal and System Analysis. La gamme de thé MORPHEE vise toute générations recherchant le sommeil paisible tant désiré et non procuré par tout types de médicaments. Essentiellement composé de feuille de morphine, ce thé vous assurera d’un rétablissement digne d’un voyage sur . PROBABILITY WORKSHOP with blocks By Jon Molomby Hands - on L wr . 2 nd’ry MATHS Q : What is the waitress asking ? Review of Terms : AND and OR HR Management Basics for the Pharmacy. Patricia A. Frame. STRATEGIES FOR HUMAN RESOURCES. Building Blocks for Success. We will cover:. WOW! Hiring.  . Retention Tactics.  . Bad Endings. #NCPA13.