PPT-Variants of Nash Equilibrium

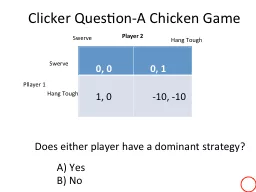
CMPT 882 Computational Game Theory Simon Fraser University Spring 2010 Instructor Oliver Schulte 1 Equilibrium Refinements A complex game may have many Nash equilibria Can we predict which one players will choose. Revision control computer program. Written by Ross Cohen with some design by Bram Cohen. Use Python. Use merging algorithm called “. Codeville. merge”. Used by . BitTorrent. , . Mosuki. Revision control. Let’s Draw a Game Tree…. Problem 6, chapter 2. Information sets in Monte Hall game. In last move, contestant knows which door he chose and which Monte opened. The door that Monte opened is neither the one that contestant opened nor the one with the good prize.. Econ 171. The Hawk-Dove Game. Animals meet encounter each other in the woods and must decide how to share a resource.. There are two possible strategies. . Hawk: Demand the entire resource and be prepared to fight for it.. Lecture 12. Constantinos Daskalakis. The Lemke-. Howson. Algorithm. The Lemke-. Howson. Algorithm (1964). Problem:. Find an exact equilibrium of a 2-player game.. Since there exists a rational equilibrium this task is feasible.. …. A) 6. B) 5. C) 4. D) 3. E) 2. Clicker Game:. Nash Equilibrium. The real John Nash. Hollywood’s Version. Clicker Question-A Chicken Game. . 0, 0. 0,. 1. . 1, 0. . -10, -10 . Econ 171. The Hawk-Dove Game. Animals meet encounter each other in the woods and must decide how to share a resource.. There are two possible strategies. . Hawk: Demand the entire resource and be prepared to fight for it.. and Best Response Functions. . Best response functions and . Nash Equilibrium. The best response function for any player . i. , is a function that maps the list of actions by other players into the list of actions that are best responses to what the others did.. . . 0, 0. 0,. . 1. . 1. , 0. . . -10, -10 . Swerve. Hang Tough. Swerve. Hang Tough. Player 2. Pllayer. 1. Does either player have a dominant strategy?. A) Yes. B) No. What’s . New here?. . Incomplete information: . Example: . Battle of the sexes . game,But. Bob . doesn’t know . what Alice wants . (i.e. her payoffs from possible outcomes). In previous examples we had “. (. Mis. )understanding. ?. Number 3.5 page 79. Answer Key claims that: . For player 1 a strictly dominates c. For player 2, y strictly dominates w and x.. These claims are correct.. The key claims that . Fall 2016. Yang Cai. Lecture . 05. Overview so far. Recap:. Games, . rationality, . solution concepts. Existence Theorems for Nash equilibrium: . Nash’s theorem for general games (via . Brouwer. Renato. . Paes. . Leme. . Éva. . Tardos. Cornell. Cornell & MSR. Keyword Auctions. organic search results. sponsored search links. Keyword Auctions. Keyword Auctions. Selling one Ad Slot. . When the rates of the forward and reverse reactions become equal, the concentrations of the reactants and the products remain constant. This is the stage of chemical equilibrium. This equilibrium is . solution concepts, and . Refinements of NASH Equilibrium. Tuomas Sandholm. The heart of the problem. In a 1-agent setting, agent. ’. s expected utility maximizing strategy is well-defined. But in a multiagent system, the outcome may depend on others.