PDF-AN INTRODUCTION TO THE SHOCK RESPONSE SPECTRUM

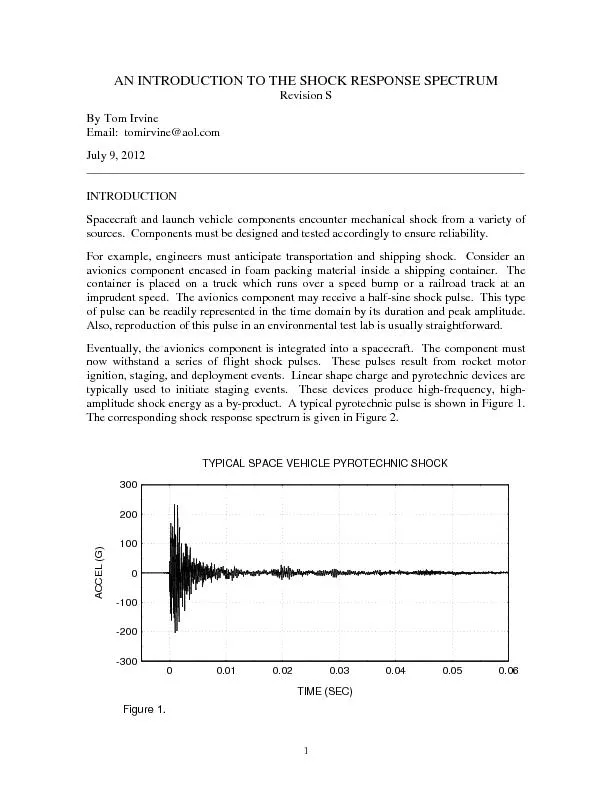
1 Revision S By Tom Irvine Email tomirvineaolcom July 9 2012 INTRODUCTION Spacecraft and launch vehicle components enco. lakeshorelearningcom response response response total recognized Writing Letters Key correctly recognized WR wrong response DK didn57557t know NR no response Key correctly written WR wrong letter written DK didn57557t know 57513 Lakeshore Alphabet C Review from Study Abroad Basics Meeting. Who do you need to talk to before studying abroad?. What do you need to do if you are a financial aid recipient?. How do credits transfer if you are not a modern language major?. Fermi Bubbles as a Scaled-up Version of Supernova . Remnants. and Predictions in the TeV Band . Yutaka Fujita (Osaka). Ryo Yamazaki (Aoyama). Yutaka Ohira (Aoyama). ApJ. L. in press (. arXiv:1308.5228. & Time History Synthesis. By Tom Irvine. 83rd Shock and Vibration Symposium 2012. This presentation is sponsored by. NASA Engineering & Safety Center (NESC. ). Dynamic Concepts, Inc.. . Huntsville, Alabama. RUSH: Overview. Early recognition and treatment of shock decreases mortality. Bedside ultrasound can rapidly evaluate for reversible causes of shock in the undifferentiated patient. Randomized, controlled trial of immediate versus delayed goal-directed ultrasound to identify the cause of . Solar Wind. , . Bow Shock. , . Magnetopause Phenomena. Christina Chu. University of Alaska Fairbanks. Geophysical Institute. -.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-. .-.-.. -. GEM Student Tutorial. 16 June 2013. Stage Separation Ground Test. Linear Shaped Charge . But fire and smoke would not occur in near-vacuum of space. Plasma jet would occur instead. Space Shuttle, Solid Rocket Booster, Frangible Nuts. “a loss of a sense of security when encountering the unfamiliar at every turn”. What differences do you expect to encounter? . Physical . -. Social . -. Worldview: values, assumptions, goals . Saccharomyces . cerevisiae. using . GRNmap. K. Grace Johnson. 1. , Margaret J. O’Neil. 2. , . Kam. D. Dahlquist. 2. , and Ben G. Fitzpatrick. 3. 1. Department of Chemistry and Biochemistry, . 2. Department of Biology, . is a . cultural. shock??. How . can. I . identify. . it. ?. What. . can. I do . about. . it. ?. What. . is. Culture shock?. I. s . the personal disorientation a person may feel when experiencing an unfamiliar way of life due to immigration or a visit to a new country, a move between social environments, or simply travel to another type of life.. William W. O’Neill, MD. Henry Ford Health System. Medical Director. Center for Structural Heart Disease. Detroit, MI. Diffuse Multivessel. Disease. . Border Zone. Dysfunction. Central Zone. Dyskinesis. spread a signal over a wide bandwidth (larger than BW in traditional communication systems). - These techniques are used for a variety of reasons, including the establishment of secure communications, increasing resistance to natural interference, noise and jamming. Paul Kolodzy, PhD. 6 April 2016. 1. CSMAC is investigating the challenges associated with spectral measurements for spectrum sharing. Moving from . non-directional transmissions . at lower frequencies to more . features introduced recently. current and near future development. 8. th. Annual European Spectrum Management Conference, 25-26 June 2013. CEPT Report 46. provides the information how EFIS is going to be improved to support the spectrum...