PDF-Incorporating "sinuous connectivity" into stochastic models of crustal

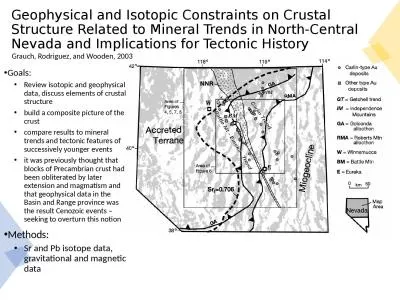
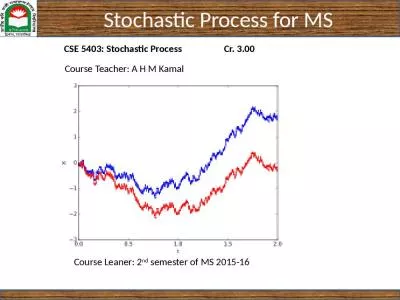
heterogeneity Examples from the Lewisian gneiss complex Scotland the Francsican formation California and the Hafafit gneiss complex Egypt John A Goff Institute for Geophysics University of T. Visualizing Crustal Thickness from active-source seismology... Why Care?. Understanding the fine details of what is happening beneath the Earth is largely an open ended scientific inquiry.. Studying the magma body below the sea floor could contribute to understanding and perhaps someday harnessing hydrothermal vents.. Inferred by Seismology. Nozomu. Takeuchi. (ERI, . Univ. of Tokyo). Importance of Directional Measurements. . from geophysicists’ point of view. (2) Improvements of Neutrino Flux Modeling. . Stochastic Calculus: Introduction . Although . stochastic . and ordinary calculus share many common properties, there are fundamental differences. The probabilistic nature of stochastic processes distinguishes them from the deterministic functions associated with ordinary calculus. Since stochastic differential equations so frequently involve Brownian motion, second order terms in the Taylor series expansion of functions become important, in contrast to ordinary calculus where they can be ignored. . plateau. Update from CIDER 2011: Dynamics of Mountain Building. Marianne Karplus. 1,2. , . Warren . Caldwell. 1. , Flora Bajolet. 3. , . Whitney . Behr. 4. , . Jiajun. . Chong. 5,6. 1 . Stanford University, . Monte Carlo Tree Search. Minimax. search fails for games with deep trees, large branching factor, and no simple heuristics. Go: branching factor . 361 (19x19 board). Monte Carlo Tree Search. Instead . Galerkin. Methods and Software. Sandia National Laboratories is a multi-program laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-AC04-94AL85000.. "QFT methods in stochastic nonlinear dynamics". ZIF, 18-19 March, 2015. D. Volchenkov. The analysis of stochastic problems sometimes might be easier than that of nonlinear dynamics – at least, we could sometimes guess upon the asymptotic solutions.. Keller and . Tackley. , 2009, Towards self-consistent modeling of the . martian. dichotomy: The influence of one-ridge convection on crustal thickness distribution, Icarus 202, 429-443. . The . dominant feature of the crustal thickness distribution obtained from one-ridge convection in the mantle is a characteristic, roughly elliptical shape that shows a striking first- order similarity to the shape of the . 1 TWTT0 s 10 s -wave reflection profile over ~1,000 km John Rundle . Econophysics. PHYS 250. Stochastic Processes. https://. en.wikipedia.org. /wiki/. Stochastic_process. In probability theory and related fields, a stochastic or random process is a mathematical object usually defined as a collection of random variables.. Goals: . Review isotopic and geophysical data, discuss elements of crustal structure. build a composite picture of the crust . compare results to mineral trends and tectonic features of successively younger events. reconstructions and tectonic implications. Randell . Stephenson et al.. A sub-crustal piercing point for North Atlantic . reconstructions and tectonic implications. Randell . Stephenson et al.. a . “tie” from one conjugate margin to . Sahil . singla. . Princeton .  Georgia Tech. Joint with . danny. . Segev. . (. Tel Aviv University). June 27. th. , 2021. Given a . Finite. . Universe : . Given an . Objective. CSE 5403: Stochastic Process Cr. 3.00. Course Leaner: 2. nd. semester of MS 2015-16. Course Teacher: A H M Kamal. Stochastic Process for MS. Sample:. The sample mean is the average value of all the observations in the data set. Usually,.