PPT-Unit III Geometric & Viewing Transformations

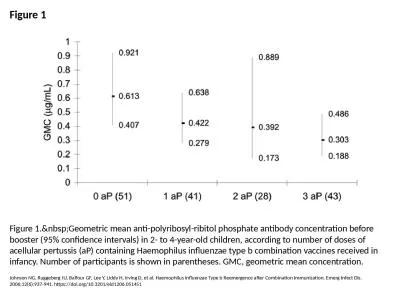
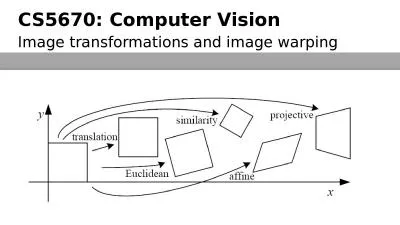
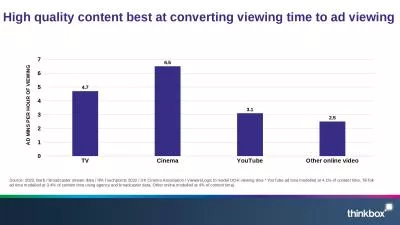
1 3D Viewing Concepts Flashback In 2D graphics applications viewing operations transfer positions from the worldcoordinate plane to pixel positions in the plane of the output device Using . 1 2D Transformations Given a point cloud polygon or sampled parametric curve w e can use transformations for several purposes 1 Change coordinate frames world window viewport devic e etc 2 Compose objects of simple parts with local scaleposition orie Pxy brPage 2br GeometricTransformations A geometric object is repres ented by its vertices as position vectors A geometric transformation is an operation that modifies its shape size position orient ation etc with respect to its current configurati Lecture 3. Jitendra. Malik. Pose and Shape. Rotations and reflections are examples. of orthogonal transformations . Rigid body motions. (Euclidean transformations / . isometries. ). Theorem:. Any rigid body motion can be expressed as an orthogonal transformation followed by a translation.. Rishabh. Singh and . Sumit. . Gulwani. FlashFill. Transformations. Syntactic Transformations . Concatenation of regular expression based substring. “VLDB2012” .  “VLDB”. Semantic Transformations. 411 Carnahan,ReynoldsandBrogan Simulation Viewing,MakingcoercibleI. Viewing,Editing,CoercingII. Viewing,LoggingEvaluatin g III. modificationExtract forInsert coercedsimulation Figure1:LifeCycleofCoerc April 13, 2016. SymphonyAM’s Suite of Solutions. 2. MediaPulse. is SymphonyAM’s patented SaaS cloud-based reporting platform housing its repository of single source cross-media data.. VideoPulse™ has dominated our focus over the last 6 months. Children 2-11, Total TV, By Daypart. Average Minute Audience (000). Average Weekly Reach (%). Average Weekly Hours Viewed (Per Cap). Average Minute Audience. Ontario, Children 2-11, By Daypart . Ontario Annual Viewing Trends. What is a Parent Function. A parent function is the most basic version of an algebraic function.. Types of Parent Functions. Linear f(x) = mx b. Quadratic f(x) = x. 2. Square Root f(x) = √x. Exponential f(x) = . Graph: .  . What is the parent function for this graph?. What does the parent function look like?. Shape is a V. Vertex is (0, 0). Slope is 1, opens up. How is the graph above different from the parent function?. . 16-385 Computer Vision. Spring 2019, . Lecture 7. http://www.cs.cmu.edu/~16385/. Course announcements. Homework 2 is posted on the course website.. - It is due on February 27. th. at 23:59 pm.. - Start early because it is much larger and more difficult than homework 1.. Johnson NG, Ruggeberg JU, Balfour GF, Lee Y, Liddy H, Irving D, et al. Haemophilus influenzae Type b Reemergence after Combination Immunization. Emerg Infect Dis. 2006;12(6):937-941. https://doi.org/10.3201/eid1206.051451. CSE 455. Ali Farhadi. Many slides from Steve Seitz and Larry . Zitnick. What are geometric transformations?. Translation. Preserves: Orientation. Translation and rotation. Scale. Similarity transformations. CS5670: Computer Vision. Reading. Szeliski. : Chapter 3.6. Announcements. Project 2 out, due Thursday, March 3 by 8pm. Do be done in groups of 2 – if you need help finding a partner, try Ed Discussions or let us know. Source: 2022, Barb / Broadcaster stream data / IPA Touchpoints 2022 / UK Cinema Association / . ViewersLogic. to model OOH viewing time * YouTube ad time modelled at 4.1% of content time, TikTok ad time modelled at 3.4% of content time using agency and broadcaster data, Other online modelled at 4% of content time).