PPT-Introduction to the Normal distribution

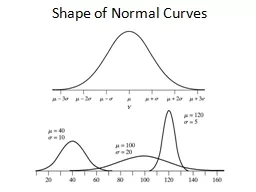
Normal random variables The Normal distribution is by far the most important and useful probability distribution in statistics with many applications in economics engineering astronomy medicine error and variation analysis etc The Normal distribution is often called the bell curve due to its distinctive shape. Harvey Goldstein. Centre for Multilevel Modelling. University of Bristol. The (multilevel) binary . probit. model. . Suppose . that we have a variance components 2-level model for . an . underlying continuous variable written as . History. Abraham de . Moivre. (1733) – consultant to . gamblers. . Pronunciation. .. Pierre Simon . Laplace – mathematician, astronomer, philosopher, determinist.. Carl Friedrich . Gauss – mathematician and astronomer.. http://www-users.york.ac.uk/~pml1/bayes/cartoons/cartoon08.jpg. 1. Comparison of Named Distributions. discrete. continuous. Bernoulli,. Binomial, Geometric, Negative Binomial, Poisson, Hypergeometric, Discrete Uniform. Distributions. Definition. Many sets of data fit what is called a Normal Distribution: EG.  . Examples when the Normal distribution arises. Looking at the national averages for NCEA.. When measuring heights, weights, arm spans, hand spans . Lesson . 2 . Starter: Find . P (. Z<1.63). To do this we begin with a sketch of the normal distribution.. We then mark a line to represent Z=1.63. P(Z<1.63) is the area under the curve to the left of a.. 2.1 Density Curves and the Normal Distributions. 2.2 Standard Normal Calculations. 2. Histogram for Strength of Yarn Bobbins. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. X. Bobbin #1: 17.15 g/tex. Normal distribution. Lognormal distribution. Mean, median and mode. Tails. Extreme value distributions. Normal (Gaussian) distribution. P. robability density function (PDF). What does figure tell about the cumulative distribution function . The Normal Curve, Skewness, Kurtosis, and Probability. VON CHRISTOPHER G. CHUA, LPT, MST. Affiliate, ESSU-Graduate School. MAED 602: STATISTICAL METHODS. Session Objectives. In this fraction of the course on Statistical Methods, graduate students enrolled in the subject are expected to do the following:. A Brief Introduction. Normal (Gaussian) Distribution. Bell-shaped distribution with tendency for individuals to clump around the group median/mean. Used to model many biological phenomena. Many . estimators . Probability Distribution. Imagine that you rolled a pair of dice. What is the probability of 5-1. ?. To answer such questions, we need to compute the whole population for possible results of rolling two dices. . z. Scores. Chapter 6. The . Bell . Curve is Born (1769). A Modern Normal Curve. Development of a Normal Curve: Sample of 5. Development of a Normal Curve: Sample of 30. Development of a Normal Curve: Sample of 140. 68%-95%-99.7% Rule. Areas under Normal Curve. Areas under Normal Curve(cont). Example: Normal Distribution. The brain weights of adult Swedish males are . approximately. normally distributed with mean μ = 1,400 g and standard deviation . . and Exponential Distributions. 5. Introduction. Several specific distributions commonly occur in a variety of business situations:. N. ormal distribution—a continuous distribution . characterized . Binomial Distribution 1. Binomial Distribution 2. Additional Problems on Binomial Distribution. More Visual Representation. Binomial Distribution Tends to Normal for Large n. Binomial Distribution Tends to Normal for p Close to 0.5.