PDF-ORIGINAL PAPER Point and interval estimates of partial population attributable risks in

Author : pamella-moone | Published Date : 2015-02-20

Spiegelman E Hertzmark H C Wand Received 8 July 2006 Accepted 28 October 2006 Springer ScienceBusiness Media BV 2007 Abstract The concept of the population attributable

Presentation Embed Code

Download Presentation

Download Presentation The PPT/PDF document "ORIGINAL PAPER Point and interval estima..." is the property of its rightful owner. Permission is granted to download and print the materials on this website for personal, non-commercial use only, and to display it on your personal computer provided you do not modify the materials and that you retain all copyright notices contained in the materials. By downloading content from our website, you accept the terms of this agreement.

ORIGINAL PAPER Point and interval estimates of partial population attributable risks in: Transcript

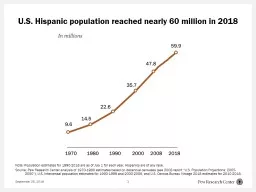
Spiegelman E Hertzmark H C Wand Received 8 July 2006 Accepted 28 October 2006 Springer ScienceBusiness Media BV 2007 Abstract The concept of the population attributable risk PAR percent has found widespread application in public health research Thi. Confidence Intervals. Lecture Summary. Last lecture, we talked about summary . statistics. and how “good” they were in estimating the . parameters. Risk, bias, and variance. Sampling distribution. An Application. Dr. Jerrell T. Stracener, . SAE Fellow. Leadership in Engineering. EMIS 7370/5370 STAT 5340 :. . . PROBABILITY AND STATISTICS FOR SCIENTISTS AND ENGINEERS. Systems Engineering Program. Bob Cohen and John Waller. 1. Postal Service Variability Ratio. and Some Implications. Ratio of attributable to institutional . c. osts from 1980 to 2013. Inframarginal costs from 2007 to 2013. 2. Significance of the Ratio. DAMPAK DALAM EPIDEMIOLOGI. Nurul. . Wandasari. . Singgih. Prodi. . Kesehatan. . Masyarakat. Univ. . Esa. . Unggul. 2012/2013. Measures of Public Health Impact. • . Attributable Risk (AR) . Confidence Intervals. (application of the Central Limit Theorem). Sections 5.1, 5.2. Introduction and Confidence Intervals for Proportions. Lecture Unit 5 Objectives. Construct . confidence intervals. 2. Overview. What are multiyear estimates?. When should you use multiyear estimates?. What should you be aware of when using multiyear estimates?. How can you use multiyear estimates to make comparisons?. Source: VAB analysis based on projected multichannel substitutes HH estimates from SNL Kagan November 2015 data and residential MVPD HH projected estimates from SNL Kagan June 2016 data which excludes DBS overlap by HHs taking multiple multichannel subscriptions. . Sample . statistics. will be slightly off from the true values of its population’s . parameters. Sampling error:. The difference between a sample statistic and a population parameter. Probability theory. . TDC Annual Conference. Austin, TX. May 26, 2017. Estimated Population Change, Texas Counties, 2010 to 2015. 2. Source: U.S. Census Bureau Population Estimates, 2015 Vintage. . 99 counties lost population over the five year period.. Note: Population estimates for 1990-2018 are as of July 1 for each year. Hispanics are of any race.. Source: Pew Research Center analysis of 1970-1980 estimates based on decennial censuses (see 2008 report “U.S. Population Projections: 2005-2050”), U.S. Intercensal population estimates for 1990-1999 and 2000-2009, and U.S. Census Bureau Vintage 2018 estimates for 2010-2018.. Analytical Observational Studies. The purpose of an analytic study in epidemiology is to identify and quantify the relationship between an exposure and a health outcome. The hallmark of such a study is the presence of at least two groups, one of which serves as a comparison group. . From the CLOSER Learning Hub. Module: Introduction to longitudinal studies. Panel studies. Follow . the same individuals over time and vary considerably in scope and . scale. Household panel studies collect information from the whole household, rather than individuals. Thanks to our funders and host institution Run major national longitudinal studiesFollow thousands of people across lifeCollect extensive & rich dataProvide free data to research community (see link 433 Open acess Manuscript accepted: August 2019 Version of record online: October 2019 J Hum Growth Dev. 2019; 29(3):433-436. DOI: https://doi.org/10.7322/jhgd.v29.9543 www. jhgd.com.br

Download Document

Here is the link to download the presentation.
"ORIGINAL PAPER Point and interval estimates of partial population attributable risks in"The content belongs to its owner. You may download and print it for personal use, without modification, and keep all copyright notices. By downloading, you agree to these terms.