PDF-DISCRETE MATHEMATICS 8 (1974)281-294.

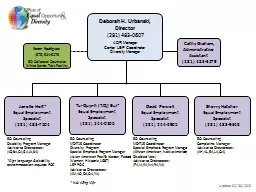
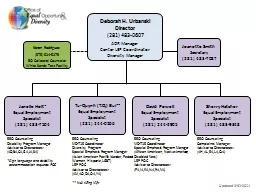
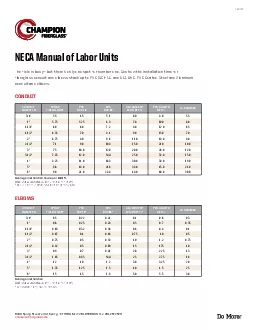
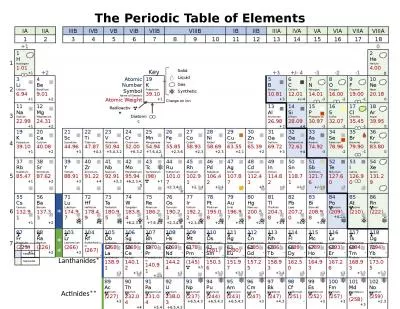
282tPErd. Give credit for both quoted and paraphrased information in a bibliography by using a consistent and sanctioned format and methodology for citations by choosing the correct use of citations and using them in their 1. . (. 281) . 483-0607. ADR Manager . Center . LEP . Coordinator. Diversity Manager . Janelle . Holt*. Equal Employment Specialist. (281) 483-7504. EO Counseling. Disability Program Manager . Advisor . Dr. Feng Gu. Way to study a system. . Cited from Simulation, Modeling & Analysis (3/e) by Law and . Kelton. , 2000, p. 4, Figure 1.1. Model taxonomy. Modeling formalisms and their simulators . Discrete time model and their simulators . 30/06/1997 To authorize the disposal of goods accepted in the course of a business for repair or other treatment but not redelivered; and for purposes connected therewith. [1 January 1970] (Original Introductory Lecture. What is Discrete Mathematics?. Discrete mathematics is the part of mathematics devoted to the study of discrete (as opposed to continuous) objects.. Calculus deals with continuous objects and is not part of discrete mathematics. . Urbanski . Director . . (. 281) . 483-0607. ADR Manager . Center . LEP . Coordinator. Diversity Manager . Janelle . Holt*. Equal Employment Specialist. (281) 483-7504. EEO . Counseling. Disability Program Manager . What year is this? 1974 1974 How long ago was that? 2013 - 1974 39 Years ago Go to page 100 of the text Go to page 100 of the text 1690 – John Locke, Natural Rights 1651 – Thomas Hobbes, Social Contract Theory November 8, 2018 Applied Discrete Mathematics Week 9: Integer Properties 1 Induction The principle of mathematical induction is a useful tool for proving that a certain predicate is true for Statistical Genomics Zhiwu Zhang Washington State University Lecture 22: Marker Assisted Selection Homework 5, due April 12, Wednesday, 3:10PM Final exam: May 4 (Thursday), 120 minutes (3:10-5:10PM), Acronyms: All School districts shall implement ELPS as an integral part of each subject in the required curriculum . The English language proficiency standards are to be published along with the Texas Essential Knowledge and Skills ( NonDisc-AccessibilityNoticeAddendum 09/2016pg 1of 4NONDISCRIMINATION AND LANGUAGE ACCESSIBILITY NOTICENondiscrimination NoticeVIVA HEALTH color national origin age disability or sex VIVA HEALTH does ELBOWSCONDUIT DIAMETEREPOXYFIBERGLASSPVCSCH 40PVCSCH 80GALVANIZEDRIGID STEELPVC-COATEDCONDUIT DIAMETER6400 Spring Stuebner Rd Spring TX 77389 Main 2816558900 Fax 2812572523championfiberglasscom kindly visit us at www.examsdump.com. Prepare your certification exams with real time Certification Questions & Answers verified by experienced professionals! We make your certification journey easier as we provide you learning materials to help you to pass your exams from the first try. Professionally researched by Certified Trainers,our preparation materials contribute to industryshighest-99.6% pass rate among our customers. +1. +2. Key. +3. +/- 4. -3. -2. -1. 2. He. Helium. 4.00. 0. 2. 3. Li. Lithium. 6.94. +1. 4. Be. Beryllium. 9.01. +2. Atomic Number. Symbol. Name of Element. Atomic Weight. 19. K. Potassium. 39.10. +1.