PDF-M Modeling the Effect of Functional Responses The functional response is refer red to

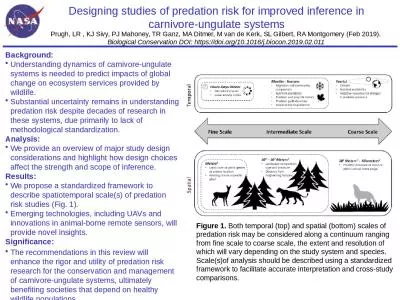
5 Modeling the Effect of Functional Responses The functional response is refer red to the predation rate as a function of the number of prey per predator It is recognized that as the number of prey increases the rat. Suharsh Sivakumar. December 11, 2010. Cellular Automaton. A grid of cells where all the cells are governed by a common set of rules based on the number of adjacent neighbors.. As generations go by, the rules work together to show very interesting phenomena in the big picture. . US Department of. Homeland Security. Predator-Prey Relationships. in Belowground Ecosystems. Goals:. Define . Predator . and. Prey . in relation to soil ecology. Define a . mathematical model. and identify some examples when one is useful. Winner takes all. Adaptive techniques predator. Keen eyesight, hearing, sense of smell and dentition suitable to killing prey.. Camouflage, which allows the predator to be concealed while hunting its prey.. Herbivory. , and Parasitism. Types of Species Interactions. When two species interact, the effects for each species can be positive, negative, or neutral.. Competition -/-. Amensalism. -/0. Commensalism +/0. Muzvondiwa J.V.. Outline. There . are a variety of . antipredator. adaptations, which suggests that predation is important in nature. Predator–prey models can explain many outcomes. Field data suggests that predators have a large impact on prey populations. 12 June 2013. Overview. Predatory pricing. Counterfactual in NZ. Criticism and proposal. Predatory Pricing. Predation Phase: lowering prices in order to foreclose competition. Recoupment Phase: Reap monopoly profits and recoup losses of predation phase. . Taylor Drexinger. Lena Finkel. David Quinn. Caroline Wilkinson . Background. Schooling vs. Shoaling. How fish school. Both advantages and disadvantages. Relevance. Impact on surrounding species. Impact on surrounding environment. Final Write up is due 9/16. Planning. Purpose/Question. :. . How does the predatory and prey relationship of ______ and _______ effect the negative feedback process seen in the natural environment?. Leslie-Gower Predator-Prey . Model. Dynamic . Behaviors of a Harvesting . Leslie-Gower Predator-Prey . Model. Na Zhang,. 1. Fengde Chen,. 1. Qianqian Su,. 1. and Ting Wu. 2. 1. College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350002, Fujian, China. meet, i.e., the chance of a lynx catching a hare.. The lynx birth rate is also proportional to how often hares & lynxes meet, i.e., the food available for each lynx family. Lynxes only die from natural causes, and their death rate is constant. D. eer Neonates in South Carolina. JOHN C. KILGO. ,1'2 USDA Forest Service, Southern Research Station, P.O. Box 700, New Ellenton, SC 29809, USA . H. SCOTT RAY. , USDA Forest Service, Savannah River, P.O. Box 700, New Ellenton, SC 20809, USA . By: Alexandra Silva and . Dani. Hoover. Intro to Systems ESE 251. 11/24/09. History. Alfred . Lotka. Vito . Volterra. -American biophysicist. -Proposed the predator-prey model in 1925. -Italian mathematician. Predator-Prey, Parasitoid-Host & Parasite-Host Relationships. “Nature red in tooth & claw”. Alfred Tennyson (1809 - 1892). Why study predation & parasitism? . A basic-science answer:. carnivore-ungulate systems. Prugh, LR , KJ . Sivy. , . PJ Mahoney, TR Ganz, MA . Ditmer. , M van de . Kerk. , SL Gilbert, RA Montgomery (Feb 2019).. Biological. Conservation. DOI:. https://doi.org/10.1016/j.biocon.2019.02.011.