PPT-Chapter 4 Sequences Section

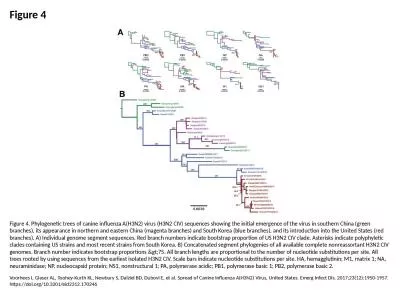
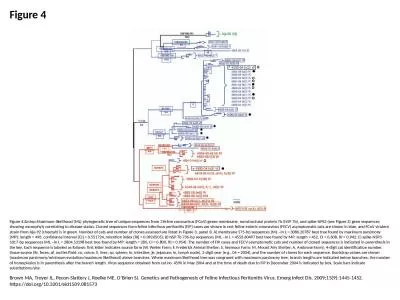
41 Convergence A sequence S is a function whose domain is the set of natural numbers We usually write s n instead of S n We may describe the sequence S as . By: Matt Connor. Fall 2013. Pure Math. Analysis. Calculus and Real Analysis . Sequences. Sequence- A list of numbers or objects in a specific order. 1,3,5,7,9,...... Finite Sequence- contains a finite number of terms. 4. Sequences and Mathematical Induction. 4.1. Sequences. Sequences. The main mathematical structure used to study repeated processes is the sequence.. The main mathematical tool used to verify conjectures about patterns governing the arrangement of terms in sequences is mathematical induction.. Places residues in columns . per . position specific similarity scores . reflects . relationships . of the . sequences. the scores are based on . indels. (gaps) and substitutions.. The alignment of residues implies that they have similar roles in the proteins or DNA sequences being aligned . Section 10.1. Sequences. Section 10.2. Infinite Series. Section 10.3. The Integral Test. 10.4. Comparison Tests. Section 10.5. Absolute Convergence; The . Ratio and Root Tests. Section 10.6. Alternating . Problem: count number of ancestors. . one has 2 parents, 4 grandparents, 8 great- grandparents, …, written in a row as. 2, 4, 8, 16, 32, 64, 128,…. To look for pattern of the numbers,. For a general value of . [ Example of one sequence and the duplication clean up for . phylo. tree will not work!!!!. >. gi|565476349|. ref|XP_006295815.1| hypothetical protein CARUB_v10024941mg [. Capsella. rubella. ] >gi|482564523. Ed Palacio, Dr. Charles Rubenstein, Bob Pellegrino. bobpellegrino@ieee.org. c.rubenstein@ieee.org. e.f.palacio@ieee.org. Agenda. Governance. -  Chair’s place in IEEE. Responsibilities, Authority, and Accountability.  Organizational linkage. Chapter 4 Sequences Section 4.2 Limit Theorems Suppose that ( s n ) and ( t n ) are convergent sequences with lim s n = s and lim t n = t . Then To simplify our work with convergent sequences, we prove several useful theorems in this section. The first theorem shows that algebraic operations are compatible with taking limits. Difference. Equations. (5.1) Sequences. (5.2) Limit of a Sequence . (5.3) Discrete Difference Equations. (5.4) Geometric & Arithmetic Sequences. (5.5) Linear Difference Equation with Constant Coefficients (scanned notes). comprise a nucleotides ACGT/U which are aligned to cognition of homologous sites is crucial if not properly established for each position incorrect trees can be inferred be done set contains few Howev Voorhees I, Glaser AL, Toohey-Kurth KL, Newbury S, Dalziel BD, Dubovi E, et al. Spread of Canine Influenza A(H3N2) Virus, United States. Emerg Infect Dis. 2017;23(12):1950-1957. https://doi.org/10.3201/eid2312.170246. Date:. 2020-09-07. September 2020. Assaf Kasher, Qualcomm. Slide . 1. Authors:. Abstract. This presentation discusses How Golay Sequences may be used for radar and sensing application and what their ambiguity function look like.. Brown MA, Troyer JL, Pecon-Slattery J, Roelke ME, O’Brien SJ. Genetics and Pathogenesis of Feline Infectious Peritonitis Virus. Emerg Infect Dis. 2009;15(9):1445-1452. https://doi.org/10.3201/eid1509.081573. Megid J, Borges IA, Abrahão JS, Trindade GS, Appolinário CM, Ribeiro MG, et al. Vaccinia Virus Zoonotic Infection, São Paulo State, Brazil. Emerg Infect Dis. 2012;18(1):189-191. https://doi.org/10.3201/eid1801.110692.