PPT-Lecture 5

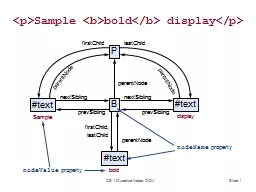
The meaning of wave function c So Hirata Department of Chemistry University of Illinois at UrbanaChampaign This material has been developed and made available online by work supported jointly by University of Illinois the National Science Foundation under Grant CHE1118616 CAREER and the Camille amp Henry Dreyfus Foundation Inc through the Camille Dreyfus TeacherScholar program Any opinions findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the sponsoring agencies. Slide . 1. <. p>Sample . <b>bold</b> display</p>. P. B. #text. #text. nextSibling. prevSibling. nextSibling. prevSibling. firstChild. lastChild. parentNode. parentNode. parentNode. Slide . 1. Google Datacenter. CS 142 Lecture Notes: Datacenters. Slide . 2. Datacenter Organization. Rack:. 50 machines. DRAM: . 800-3200GB . @ 300 . µs. Disk: 100TB @ 10ms. Single server:. 8-24 . cores. Sensors. (bit incomplete. , still). Sensing Categories. Voltage. starting easy: analog in. Distance. acoustic or light. Speed. hard; usu. via distance. Acceleration. accelerometers. Light Level. phototransistors, photodiodes. and Brian Voigt © 2011, . except where noted. Lecture 6:. Introduction to Projections and Coordinate Systems. By Austin Troy and Brian Voigt, University of Vermont,. with sections adapted from ESRI’s online course on projections. Assembly Language and . Arduino. Behind the C code (or sketch). C provides a somewhat human-readable interface. but it gets . compiled. into machine instruction set. ultimately just binary (or hex) instructions loaded into the . Intro to IT. . COSC1078 Introduction to Information Technology. . Lecture 5. Audio. James Harland. james.harland@rmit.edu.au. Lecture . 5: Audio. Intro to IT. . Introduction. James Harland. Email:. with. Students. Carl S. Moore, Assistant Director . Carl.moore@temple.edu. Teaching and Learning Center. Temple University . Wood, D., Bruner, J. S., & Ross, G. (1976). The Role of Tutoring in Problem Solving*. Journal of child psychology and psychiatry, 17(2), 89-100.. 1. The LHC Voyage . Of. Discovery . Dan Green. Fermilab. Fermilab Lecture, Sept. 23, 2011. 2. What is Particle Physics?. Particle physics is the modern name for the centuries old effort to understand the laws of nature. . Slide . 1. <. p>Sample . <b>bold</b> display</p>. P. B. #text. #text. nextSibling. prevSibling. nextSibling. prevSibling. firstChild. lastChild. parentNode. parentNode. parentNode. Slide . 1. Intelligent Systems (AI-2). Computer Science . cpsc422. , Lecture . 11. Oct, 2, . 2015. 422 . big . picture: Where are we?. Query. Planning. Deterministic. Stochastic. Value Iteration. Approx. Inference. More than Just Capturing Lectures. Bill King. What is Lecture Capture?. Lecture Capture is the use of a set of technologies to capture and then enable time-shifted and place-shifted viewing of the Lecture Content.. Assembly Language and . Arduino. Adapted from T. Murphy’s slides. Behind the C code (or sketch). C provides a somewhat human-readable interface. but it gets . compiled. into machine instruction set. In online and blended learning platforms. An experiment with technology . Margaret Conlon. Edinburgh Napier University. Regularly used in dazzlingly large lectures….. But received some criticism…. Slide . 1. CSS Rule. body {. font-family: Tahoma, Arial, sans-serif;. color: black;. background: white;. margin: 8px;. }. Selector. Declaration. Block. Attribute Name. Value. CS 142 Lecture Notes: CSS.